
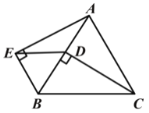
【题目】如图,△ABC是等边三角形,CD⊥AB于点D,∠AEB=90°,CD=AE.
求证:(1)△BCD≌△BAE;(2)△EBD是等边三角形.
科目:初中数学 来源: 题型:
【题目】某次篮球联赛初赛阶段,每队有![]() 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得![]() 分, 负一场得
分, 负一场得![]() 分,积分超过
分,积分超过![]() 分才能获得参赛资格.
分才能获得参赛资格.
(1)已知甲队在初赛阶段的积分为![]() 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
查看答案和解析>>
科目:初中数学 来源: 题型:
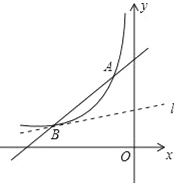
【题目】(2016广东省茂名市)如图,一次函数y=x+b的图象与反比例函数![]() (k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).
(k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).
(1)求反比例函数的表达式和a、b的值;
(2)若A、O两点关于直线l对称,请连接AO,并求出直线l与线段AO的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
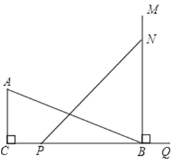
【题目】如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_______秒时,△BCA与点P、N、B为顶点的三角形全等.(2个全等三角形不重合)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,点O是△ABC内的一点,∠BOC=130°.
(1)求证:OB=DC;
(2)求∠DCO的大小;
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
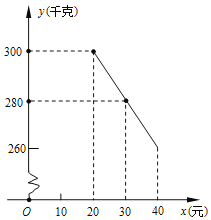
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x 的函数关系图象.
(1)求y与x的函数关系式;
(2)直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
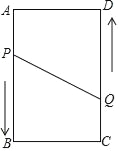
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形APQD为长方形?
(2)P、Q两点从出发开始到几秒时?四边形PBCQ的面积为33cm2;
(3)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平行四边形ABCD,求作菱形AECF,使点E、点F分别在BC、AD边上
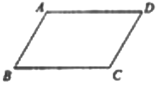
下面是小明设计的尺规作图过程.
作法:如图
① 连接AC;
② 分别以A、C为圆心,大于![]() AC的长为半径作弧,两弧交于M、N两点;
AC的长为半径作弧,两弧交于M、N两点;
③ 连接MN,分别与BC、AD、AC交于E、F、O三点;
④ 连接AE、CF
四边形AECF即为所求
根据小明设计的尺规作图过程
(1)使用直尺和圆规,补全图形:(保留作图痕迹)
(2)完成下面的证明
证明∵AM= ,AN= ,
∴MN是AC的垂直平分线。
( )(填推理的依据)
∴EF⊥AC,OA=OC,
∴平行四边形ABCD
∴AD∥BC
∴∠FAO=∠ECO
在△FAO和△ECO中

∴△FAO≌△ECO
∴OE=OF
又∵OA=OC
∴四边形AECF是平行四边形
( )(填推理依据)
∵EF⊥AC
∴四边形AECF是菱形
( )(填推理依据)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com