
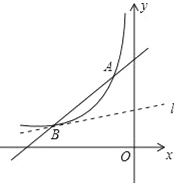
【题目】(2016广东省茂名市)如图,一次函数y=x+b的图象与反比例函数![]() (k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).
(k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).
(1)求反比例函数的表达式和a、b的值;
(2)若A、O两点关于直线l对称,请连接AO,并求出直线l与线段AO的交点坐标.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)(
;(2)(![]() ,2).
,2).
【解析】
试题(1)由点A的坐标结合反比例函数图象上点的坐标特征,即可求出k值,从而得出反比例函数解析式;再将点A、B坐标分别代入一次函数y=x+b中得出关于a、b的二元一次方程组,解方程组即可得出结论;(2)连接AO,设线段AO与直线l相交于点M.由A、O两点关于直线l对称,可得出点M为线段AO的中点,再结合点A、O的坐标即可得出结论.
试题解析:(1)∵点A(﹣1,4)在反比例函数y=![]() (k为常数,k≠0)的图象上,
(k为常数,k≠0)的图象上,
∴k=﹣1×4=﹣4, ∴反比例函数解析式为y=﹣![]()
把点A(﹣1,4)、B(a,1)分别代入y=x+b中,
得:![]() ,解得:
,解得:![]() .
.
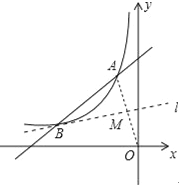
(2)连接AO,设线段AO与直线l相交于点M,如图所示. ∵A、O两点关于直线l对称,
∴点M为线段OA的中点, ∵点A(﹣1,4)、O(0,0), ∴点M的坐标为(﹣![]() ,2).
,2).
∴直线l与线段AO的交点坐标为(﹣![]() ,2).
,2).


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠B=90![]() ,∠ACB=30
,∠ACB=30![]() ,AB=2,AD=2AC,DC=2BC.
,AB=2,AD=2AC,DC=2BC.
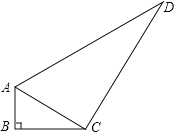
(1)求证:△ACD为直角三角形;(2)求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
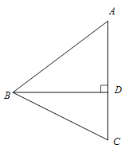
【题目】如图,在△ABC中,AB=AC>BC,BD 是AC边上的高,点C关于直线BD的对称点为点E,连接BE.
(1)①依题意补全图形;
②若∠BAC=![]() ,求∠DBE的大小(用含
,求∠DBE的大小(用含![]() 的式子表示);
的式子表示);
(2)若DE=2AE,点F是BE中点,连接AF,BD=4,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
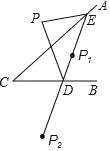
【题目】如图,点P是直线AC外的一点,点D,E分别是AC,CB两边上的点,点P关于CA的对称点P1恰好落在线段ED上,P点关于CB的对称点P2落在ED的延长线上,若PE=2.5,PD=3,ED=4,则线段P1P2的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=m,P为BC上任意一点,则PA2+PBPC的值为( )
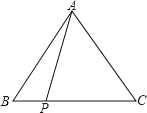
A. m2 B. m2+1 C. 2m2 D. (m+1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家新开发的一种电动车如图,它的大灯A射出的光线AB,AC与地面MN所夹的锐角分别为8°和10°,大灯A与地面离地面的距离为1m求该车大灯照亮地面的宽度BC.(不考虑其它因素)(参数数据:sin8°=![]() ,tan8°=
,tan8°=![]() ,sin10°=
,sin10°=![]() ,tan10°=
,tan10°=![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com