
【题目】已知![]() ,
,![]() ,
,![]() 为正整数,
为正整数,![]() .设
.设![]() ,
,![]() ,
,![]() ,
,![]() 为坐标原点.若
为坐标原点.若![]() ,且
,且![]() .
.
(1)求图象经过![]() ,
,![]() ,
,![]() 三点的二次函数的解析式;
三点的二次函数的解析式;
(2)点![]() 是抛物线上的一动点,直线
是抛物线上的一动点,直线![]() 交线段
交线段![]() 于点
于点![]() ,若
,若![]() ,
,![]() 的面积
的面积![]() ,
,![]() 满足
满足![]() ,求此时点
,求此时点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由射影定理得到![]() ,即
,即![]() ,然后代入到已知条件中得到
,然后代入到已知条件中得到![]() ,然后利用一元二次方程根与系数的关系求得
,然后利用一元二次方程根与系数的关系求得![]() ,
,![]() .利用待定系数法求二次函数解析式;
.利用待定系数法求二次函数解析式;
(2)由![]() 得
得![]() ,从而确定Q点坐标,然后利用待定系数法求得直线AQ的解析式,然后联立方程组求点D坐标.
,从而确定Q点坐标,然后利用待定系数法求得直线AQ的解析式,然后联立方程组求点D坐标.
解:(1)∵![]() ,
,![]() ,∴
,∴![]() ,即
,即![]() .
.
∵![]() ,
,
∴![]() .
.
又∵![]()
![]() ,
,
![]()
![]()
∴![]() ,即
,即![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() ①的两个不相等的正整数根,
①的两个不相等的正整数根,
∴![]() ,解得
,解得![]() .
.
又∵![]() 为正整数,故
为正整数,故![]() 或
或![]() .
.
当![]() 时,方程①为
时,方程①为![]() ,没有整数解.
,没有整数解.
当![]() 时,方程①为
时,方程①为![]() ,两根为
,两根为![]() ,
,![]() .
.
综合知:![]() ,
,![]() ,
,![]() .
.
设图象经过![]() ,
,![]() ,
,![]() 三点的二次函数的解析式为
三点的二次函数的解析式为![]() ,
,
将点![]() 的坐标代入得
的坐标代入得![]() ,解得
,解得![]() .
.
∴图象经过![]() ,
,![]() ,
,![]() 三点的二次函数的解析式为
三点的二次函数的解析式为![]() .
.
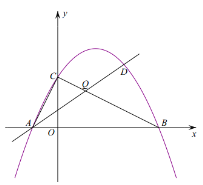
(2)如图,直线![]() 交线段
交线段![]() 于点
于点![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,∵
,∵![]() ,
,
设直线AQ的解析式为y=kx+b
可得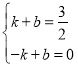 解得
解得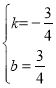
∴直线AQ的解析式为:![]() ,
,
联立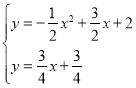 ,
,
消去![]() 整理可得,
整理可得,![]() ,
,
由韦达定理:![]() ,而
,而![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() 点坐标为:
点坐标为:![]() .
.


科目:初中数学 来源: 题型:
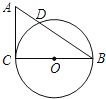
【题目】如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问:当点E在什么位置时,直线ED与⊙O相切?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2mx+m2﹣3(m是常数)
(1)证明:无论m取什么实数,该抛物线与x轴都有两个交点.
(2)设抛物线的顶点为A,与x轴的两个交点分别为B、D,点B在点D的右侧,与y轴的交点为 C.
①若点P为△ABD的外心,求点P的坐标(用含m的式子表示);
②当|m|≤![]() ,m≠0时,△ABC的面积是否有最大值?如果有,请求出最大值;如果没有,请说明理由.
,m≠0时,△ABC的面积是否有最大值?如果有,请求出最大值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销A、B两种商品,现有如下信息:
信息1:A、B两种商品的进货单价之和是3元;
信息2:A商品零售单价比进货单价多1元,B商品零售单价比进货单价的2倍少1元;
信息3:按零售单价购买A商品3件和B商品2件,共付12元.
请根据以上信息,解答下列问题:
(1)求A、B两种商品的零售单价;
(2)该商店平均每天卖出A商品500件和B商品1500件.经调查发现,A种商品零售单价每降0.1元,A种商品每天可多销售100件.商店决定把A商品的零售单价下降m(m>0)元,B商品的零售单价和销量都不变,在不考虑其他因素的条件下,当m为多少时,商品每天销售A、B两种商品获取的总利润为2000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张如图所示的长为![]() ,宽为
,宽为![]() 的小长方形纸片,按如图的方式不重叠地放在矩形
的小长方形纸片,按如图的方式不重叠地放在矩形![]() 中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为
中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为![]() ,当
,当![]() 的长度变化时,按照同样的放置方式,
的长度变化时,按照同样的放置方式,![]() 始终保持不变,则
始终保持不变,则![]() ,
,![]() 满足的关系式为( )
满足的关系式为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
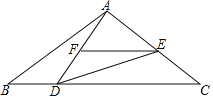
【题目】如图:已知在△ABC中,AB=AC,点D是BC上一点,∠ADE=∠B,
(1)求证:△ABD~△DCE;
(2)点F在AD上,且![]() =
=![]() ,求证:EF∥CD.
,求证:EF∥CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华星商店准备从阳光机械厂购进甲、乙两种零件进行销售,若一个甲种零件的进价比一个乙种零件的进价多50元,用4000元购进甲种零件的数量是用1500元购进乙种零件的数量的2倍.
(1)求每个甲种零件,每个乙种零件的进价分别为多少元?
(2)华星商店甲种零件每件售价为260元,乙种零件每件售价为190元,商店根据市场需求.决定向该厂购进一批零件、且购进乙种零件的数量比购进甲种零件的数量的2倍还多4个,若本次购进的两种零件全部售出后,总获利不少于2400元、求该商店本次购进甲种零件至少是多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中 xOy 中,对于⊙C及⊙C内一点 P,给出如下定义:若存在过点 P 的直线 l,使得它与⊙C 相交所截得的弦长为![]() ,则称点 P 为⊙C的“k-近内点”.
,则称点 P 为⊙C的“k-近内点”.
(1)已知⊙O的半径为 4,
①在点中![]() ,⊙O的“4-近内点”是______________;
,⊙O的“4-近内点”是______________;
②点 P 在直线y=![]() x上,若点 P 为⊙O的“4-近内点”,则点 P 的纵坐标y的取值范围是____________;
x上,若点 P 为⊙O的“4-近内点”,则点 P 的纵坐标y的取值范围是____________;
(2)⊙C的圆心为(-1,0),半径为 3,直线![]() x 轴,y 轴分别交于 M,N,若线段 MN 上存在⊙C的 “2
x 轴,y 轴分别交于 M,N,若线段 MN 上存在⊙C的 “2![]() -近内点”,则 b 的取值范围是____________.
-近内点”,则 b 的取值范围是____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com