
【题目】已知抛物线y=x2﹣2mx+m2﹣3(m是常数)
(1)证明:无论m取什么实数,该抛物线与x轴都有两个交点.
(2)设抛物线的顶点为A,与x轴的两个交点分别为B、D,点B在点D的右侧,与y轴的交点为 C.
①若点P为△ABD的外心,求点P的坐标(用含m的式子表示);
②当|m|≤![]() ,m≠0时,△ABC的面积是否有最大值?如果有,请求出最大值;如果没有,请说明理由.
,m≠0时,△ABC的面积是否有最大值?如果有,请求出最大值;如果没有,请说明理由.
【答案】(1)证明见解析;(2)①P(m,-1);②有最大值;当m=![]() 时,S△ABC最大=3
时,S△ABC最大=3![]() .
.
【解析】
(1)令y=0,转化成一元二次方程,计算判别式,可得判别式的值大于0,即可得出结论;
(2)①先求出点A的坐标,再求出BD的长,进而得出BE的长,再利用勾股定理求出外接圆的半径,即可得出结论;②先求出点B的坐标,点C的坐标,分两种情况:(i)当0<m≤![]() 时,如图2,(ii)当-
时,如图2,(ii)当-![]() ≤m<0时,如图3,分别得出S与m的函数关系式,即可得出结论.
≤m<0时,如图3,分别得出S与m的函数关系式,即可得出结论.
(1)令y=0,则0=x2﹣2mx+m2﹣3,
∴△=(﹣2m)2﹣4(m2﹣3)=12>0,
∴方程x2﹣2mx+m2﹣3=0有两个不相等的实数根,
即:无论m取什么实数,该抛物线与x轴都有两个交点;
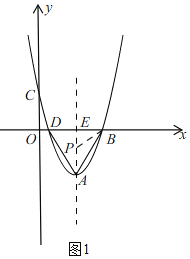
(2)①如图1,
∵抛物线y=x2﹣2mx+m2﹣3=(x﹣m)2﹣3,
∴A(m,﹣3),设点D(x1,0),B(x2,0),
∴x1+x2=2m,x1x2=m2﹣3,
∴BD=x2﹣x1=![]() =
=![]() =2
=2![]() ,
,
过点A作平行于y轴的直线,交x轴于点E,则AE⊥x轴,
∴∠AEB=90°,
∵点A(m,﹣3)是抛物线的顶点,
∴AE=3,BE=![]() BD=
BD=![]() ,
,
∴P为△ABD的外心,
∴点P在AE上,
连接BP,
设△ABD的外接圆的半径为r,则AP=BP=r,
∴PE=AE﹣r=3﹣r,
∵在Rt△BEP中, PE2+BE2=BP2,
∴(3﹣r)2+(![]() )2=r2,
)2=r2,
∴r=2,
∴PE=AE﹣AP=1,
∴P(m,-1);
②令y=0,则x2﹣2mx+m2﹣3=0,
∴x=![]() ,
,
∵点B在点D的右侧,
∴B(m+![]() ,0),D(m-
,0),D(m-![]() ,0),
,0),
令x=0,则y=m2﹣3,
∴C(0,m2﹣3),
分两种情况考虑:
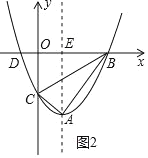
(i)当0<m≤![]() 时,如图2,
时,如图2,
S△ABC=S梯形OCAE+S△ABES△OCB
=![]() OE(OC+AE)+
OE(OC+AE)+ ![]() AEBE
AEBE![]() OCOB
OCOB
=![]() m(3m2+3)+
m(3m2+3)+ ![]() ×3×(m+
×3×(m+![]() m)
m) ![]() (3m2)(m+
(3m2)(m+![]() )
)
=![]() m2+
m2+![]() m
m
=![]() (m +
(m +![]() )2﹣
)2﹣![]() ,
,
∵![]() >0,
>0,
∴当0<m≤![]() 时,S△ABC随m的增大而增大,
时,S△ABC随m的增大而增大,
∴当m=![]() 时,S△ABC取得最大值,最大值为3
时,S△ABC取得最大值,最大值为3![]() ;
;
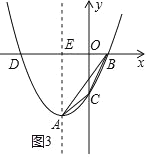
(ii)当-![]() ≤m<0时,如图3,
≤m<0时,如图3,
S△ABC=S梯形EACO+S△OCBS△ABE
=![]() OE(OC+AE)+
OE(OC+AE)+ ![]() OCOB
OCOB![]() AEBE
AEBE
=![]() m(3m2+3)+
m(3m2+3)+ ![]() (3m2)(m+
(3m2)(m+![]() )
)![]() (m+
(m+![]() m)(3m2)
m)(3m2)
=![]() m,
m,
∵![]() <0,
<0,
∴当-![]() ≤m<0时,S△ABC随m的增大而减小,
≤m<0时,S△ABC随m的增大而减小,
∴当m=-![]() 时,S△ABC取得最大值,最大值为
时,S△ABC取得最大值,最大值为![]() .
.
∵3![]() >
>![]() ,
,
∴当m=![]() 时,△ABC的面积取得最大值,最大值为3
时,△ABC的面积取得最大值,最大值为3![]() .
.


科目:初中数学 来源: 题型:
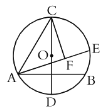
【题目】如图,在半径为4的![]() 中,
中,![]() 为直径,弦
为直径,弦![]() 且过半径
且过半径![]() 的中点,
的中点,![]() 为
为![]() 上一动点,
上一动点,![]() 于点
于点![]() ,即点
,即点![]() 在以
在以![]() 为直径的圆上,当
为直径的圆上,当![]() 从点
从点![]() 出发顺时针运动到点
出发顺时针运动到点![]() 时,点
时,点![]() 所经过的路径长为( )
所经过的路径长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在 10×6 的正方形网格中,每个小正方形的边长均为 1,线段 AB 的端点 A、B 均在小正方形的顶点上.
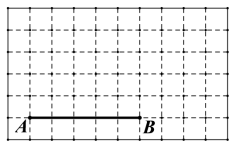
(1)在图中画出以 AB 为一腰的等腰△ABC,点 C 在小正方形顶点上,△ABC 为钝角三角形,且△ABC 的面积为![]() ;
;
(2)在图中画出以 AB 为斜边的直角三角形 ABD, 点 D在小正方形的顶点上,且 AD>BD;
(3)连接 CD,请你直接写出线段 CD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一节数学活动课上,王老师将本班学生身高数据(精确到1厘米)出示给大家,要求同学们各自独立绘制一幅频数分布直方图,甲绘制的如图①所示,乙绘制的如图②所示,经王老师批改,甲绘制的图是正确的,乙在数据整理与绘图过程中均有个别错误.
(1)写出乙同学在数据整理或绘图过程中的错误(写出一个即可);
(2)甲同学在数据整理后若用扇形统计图表示,则159.5﹣164.5这一部分所对应的扇形圆心角的度数为 ;
(3)该班学生的身高数据的中位数是 ;
(4)假设身高在169.5﹣174.5范围的5名同学中,有2名女同学,班主任老师想在这5名同学中选出2名同学作为本班的正、副旗手,那么恰好选中一名男同学和一名女同学当正,副旗手的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
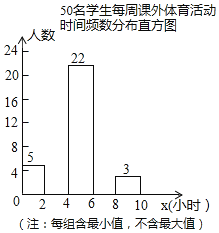
【题目】为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:
(1)本次调查样本容量是 ;
(2)请补全频数分布直方图中空缺的部分;
(3)估计全校学生每周课外体育活动时间不少于6小时的人数.
(4)求这50名学生每周课外体育活动时间的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
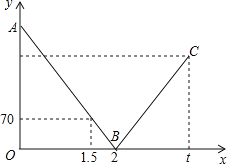
【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),如图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,则t的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() 为正整数,
为正整数,![]() .设
.设![]() ,
,![]() ,
,![]() ,
,![]() 为坐标原点.若
为坐标原点.若![]() ,且
,且![]() .
.
(1)求图象经过![]() ,
,![]() ,
,![]() 三点的二次函数的解析式;
三点的二次函数的解析式;
(2)点![]() 是抛物线上的一动点,直线
是抛物线上的一动点,直线![]() 交线段
交线段![]() 于点
于点![]() ,若
,若![]() ,
,![]() 的面积
的面积![]() ,
,![]() 满足
满足![]() ,求此时点
,求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
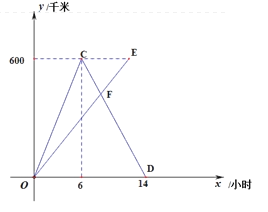
【题目】甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)AB两城之间的距离为_______km.
(2)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(3)乙用8小时到达B城,求乙车速度及他们相遇的时间.
(4)直接写出两车何时相距80km?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com