练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

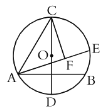
    【题目】如图，在半径为4的中，为直径，弦且过半径的中点，为上一动点，于点，即点在以为直径的圆上，当从点出发顺时针运动到点时，点所经过的路径长为（ ）

    A.B.C.D.

    【答案】C

    【解析】

    先找到当E与B、D重合时相应的F点、，因为在以为直径的圆上，所以劣弧即为点所经过的路径，连AO，由，得，依据同弧所对的圆心角是圆周角的两倍，得到，，运用锐角三角函数求出，依据有一个角为60度的等腰三角形是等边三角形，可得是等边三角形，从而，最后用弧长公式计算即可.

    解：∵为直径，

    ∴于点，

    如图，取的中点为，

    ∵当E与B重合时，于点，当E与D重合时，于点，

    ∴劣弧即为点所经过的路径，

    连AO，

    ∵,

    ∴

    ∴，，

    ∴，，

    ∵，，

    ∴是等边三角形，,

    ∴==，

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知抛物线经过两点．

    （1）求抛物线的解析式和顶点坐标；

    （2）设点为抛物线上一点，若，求点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为加快5G网络建设，某移动通信公司在一个坡度为2：1的山腰上建了一座5G信号通信塔AB，在距山脚C处水平距离39米的点D处测得通信塔底B处的仰角是35°，测得通信塔顶A处的仰角是49°，(参考数据：sin35°≈0.57，tan35°≈0.70，sin49°≈0.75，tan49°≈1.15)，则通信塔AB的高度约为( )

    A.27米B.31米C.48米D.52米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知∠MON＝120°，点A，B分别在ON，OM边上，且OA＝OB，点C在线段OB上（不与点O，B重合），连接CA．将射线CA绕点C逆时针旋转120°得到射线CA′，将射线BO绕点B逆时针旋转150°与射线CA′交于点D．

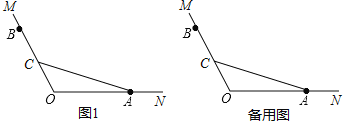
    （1）根据题意补全图1；

    （2）求证：

    ①∠OAC＝∠DCB；

    ②CD＝CA（提示：可以在OA上截取OE＝OC，连接CE）；

    （3）点H在线段AO的延长线上，当线段OH，OC，OA满足什么等量关系时，对于任意的点C都有∠DCH＝2∠DAH，写出你的猜想并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB是的直径，点P在BA的延长线上，PD切于点D，过点B作，交PD的延长线于点C，连接AD并延长，交BE于点E．

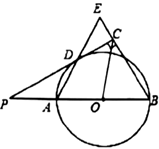
    (Ⅰ)求证：AB=BE；

    (Ⅱ)连结OC，如果PD=2，∠ABC=60°，求OC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于的一元二次方程x2-(k+2)x+k-1=0

    （1）若方程的一个根为 -1，求的值和方程的另一个根；

    （2）求证：不论取何值，该方程都有两个不相等的实数根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为迎接“六一”儿童节，某儿童品牌玩具专卖店购进了A、B两种玩具，其中A类玩具的进价比B玩具的进价每个多3元，经调查：用900元购进A类玩具的数量与用750元购进B类玩具的数量相同

    （1）求A、B两类玩具的进价分别是每个多少元？

    （2）该玩具店共购进了A、B两类玩具共100个，若玩具店将每个A类玩具定价为30元出售，每个B类玩具定价25元出售，且全部售出后所获得利润不少于1080元，则商店至少购进A类玩具多少个？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

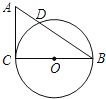
    【题目】如图，在Rt△ACB中，∠C=90°，AC=3cm，BC=4cm，以BC为直径作⊙O交AB于点D．

    （1）求线段AD的长度；

    （2）点E是线段AC上的一点，试问：当点E在什么位置时，直线ED与⊙O相切？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y＝x2﹣2mx+m2﹣3（m是常数）

    （1）证明：无论m取什么实数，该抛物线与x轴都有两个交点．

    （2）设抛物线的顶点为A，与x轴的两个交点分别为B、D，点B在点D的右侧，与y轴的交点为 C．

    ①若点P为△ABD的外心，求点P的坐标（用含m的式子表示）；

    ②当|m|≤，m≠0时，△ABC的面积是否有最大值？如果有，请求出最大值；如果没有，请说明理由．

    查看答案和解析>>

    同步练习册答案