
【题目】为加快5G网络建设,某移动通信公司在一个坡度为2:1的山腰上建了一座5G信号通信塔AB,在距山脚C处水平距离39米的点D处测得通信塔底B处的仰角是35°,测得通信塔顶A处的仰角是49°,(参考数据:sin35°≈0.57,tan35°≈0.70,sin49°≈0.75,tan49°≈1.15),则通信塔AB的高度约为( )
A.27米B.31米C.48米D.52米
【答案】A
【解析】
根据题意画出图形,延长AB交DC延长线于点E,设CE=x、则BE=2x、DE=39+x,由tan∠BDE=![]() 求得x=21,即可知DE=39+x=60、BE=2x=42,再由AE=DEtan∠ADE=69,根据AB=AE﹣BE可得答案.
求得x=21,即可知DE=39+x=60、BE=2x=42,再由AE=DEtan∠ADE=69,根据AB=AE﹣BE可得答案.
解:如图所示,延长AB交DC延长线于点E,则∠DEA=90°,
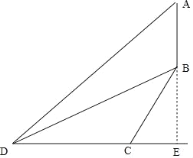
由题意知∠DBC=35°、∠ADE=49°、CD=39米,BC的坡度为2:1
设CE=x、则BE=2x、DE=39+x,
由tan∠BDE=![]() 可得
可得![]() ≈0.7,
≈0.7,
解得:x=21,
∴DE=39+x=60、BE=2x=42,
在Rt△ADE中,AE=DEtan∠ADE≈60×1.15=69,
则AB=AE﹣BE=69﹣42=27(米),
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
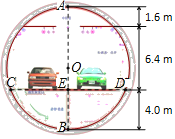
【题目】如图,是一张盾构隧道断面结构图.隧道内部为以O为圆心,AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为1.6m,顶棚到路面的距离是6.4m,点B到路面的距离为4.0m.请求出路面CD的宽度.(精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的弦,∠OAB=45°,C是优弧AB上的一点,BD∥OA,交CA延长线于点D,连接BC.
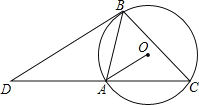
(1)求证:BD是⊙O的切线;
(2)若AC=![]() ,∠CAB=75°,求⊙O的半径.
,∠CAB=75°,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知k为实数,关于x的方程为x2+(k+2)x+2k=1.
(1)判断方程有无实数根.
(2)当方程的根和k都是有理数时,请直接写出其中k的1个值和相应方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
⑴请你补全这个输水管道的圆形截面;
⑵若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=10.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边经过点C,另一直角边AB交于点E.
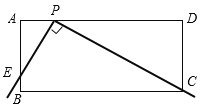
(1)求证:![]()
(2)是否存在这样的点P,使![]() 的周长等于
的周长等于![]() 周长的2倍?若存在,求出DP的长;若不存在,请说明理由.
周长的2倍?若存在,求出DP的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“衍生直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“衍生三角形”.已知抛物线![]() 与其“衍生直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“衍生直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.

(1)填空:该抛物线的“衍生直线”的解析式为 ,点A的坐标为 ,点B的坐标为 ;
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“衍生三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“衍生直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com