
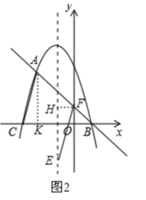
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЮвУЧЖЈвхжБЯпy=ax-aЮЊХзЮяЯпy=ax2+bx+cЃЈaЁЂbЁЂcЮЊГЃЪ§ЃЌaЁй0ЃЉЕФЁАбмЩњжБЯпЁБЃЛгавЛИіЖЅЕудкХзЮяЯпЩЯЃЌСэгавЛИіЖЅЕудкyжсЩЯЕФШ§НЧаЮЮЊЦфЁАбмЩњШ§НЧаЮЁБЃЎвбжЊХзЮяЯп![]() гыЦфЁАбмЩњжБЯпЁБНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыxжсИКАыжсНЛгкЕуCЃЎ
гыЦфЁАбмЩњжБЯпЁБНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыxжсИКАыжсНЛгкЕуCЃЎ

ЃЈ1ЃЉЬюПеЃКИУХзЮяЯпЕФЁАбмЩњжБЯпЁБЕФНтЮіЪНЮЊ ЃЌЕуAЕФзјБъЮЊ ЃЌЕуBЕФзјБъЮЊ ЃЛ
ЃЈ2ЃЉШчЭМЃЌЕуMЮЊЯпЖЮCBЩЯвЛЖЏЕуЃЌНЋЁїACMвдAMЫљдкжБЯпЮЊЖдГЦжсЗелЃЌЕуCЕФЖдГЦЕуЮЊNЃЌШєЁїAMNЮЊИУХзЮяЯпЕФЁАбмЩњШ§НЧаЮЁБЃЌЧѓЕуNЕФзјБъЃЛ
ЃЈ3ЃЉЕБЕуEдкХзЮяЯпЕФЖдГЦжсЩЯдЫЖЏЪБЃЌдкИУХзЮяЯпЕФЁАбмЩњжБЯпЁБЩЯЃЌЪЧЗёДцдкЕуFЃЌЪЙЕУвдЕуAЁЂCЁЂEЁЂFЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуEЁЂFЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ-2ЃЌ
ЃЛЃЈ-2ЃЌ![]() ЃЉЃЛЃЈ1,0ЃЉЃЛ
ЃЉЃЛЃЈ1,0ЃЉЃЛ
ЃЈ2ЃЉNЕуЕФзјБъЮЊЃЈ0ЃЌ![]() ЃЉЃЌЃЈ0ЃЌ
ЃЉЃЌЃЈ0ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉEЃЈ-1ЃЌ-![]() ЃЉЁЂFЃЈ0ЃЌ
ЃЉЁЂFЃЈ0ЃЌ![]() ЃЉЛђEЃЈ-1ЃЌ
ЃЉЛђEЃЈ-1ЃЌ![]() ЃЉЃЌFЃЈ-4ЃЌ
ЃЉЃЌFЃЈ-4ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩХзЮяЯпЕФЁАбмЩњжБЯпЁБжЊЕРЖўДЮКЏЪ§НтЮіЪНЕФaМДПЩЃЛЃЈ2ЃЉЙ§AзїADЁЭyжсгкЕуDЃЌдђПЩжЊAN=ACЃЌНсКЯAЕузјБъЃЌдђПЩЧѓГіONЕФГЄЃЌПЩЧѓГіNЕуЕФзјБъЃЛЃЈ3ЃЉЗжБ№ЬжТлЕБACЮЊЦНааЫФБпаЮЕФБпЪБЃЌЕБACЮЊЦНааЫФБпаЮЕФЖдНЧЯпЪБЃЌЧѓГіТњзуЬѕМўЕФEЁЂFзјБъМДПЩ
ЃЈ1ЃЉЁп![]() ЃЌa=
ЃЌa=![]() ЃЌдђХзЮяЯпЕФЁАбмЩњжБЯпЁБЕФНтЮіЪНЮЊ
ЃЌдђХзЮяЯпЕФЁАбмЩњжБЯпЁБЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
СЊСЂСННтЮіЪНЧѓНЛЕу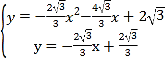 ЃЌНтЕУ
ЃЌНтЕУ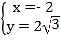 Лђ
Лђ![]() ЃЌ
ЃЌ
ЁрAЃЈ-2ЃЌ![]() ЃЉЃЌBЃЈ1,0ЃЉЃЛ
ЃЉЃЌBЃЈ1,0ЃЉЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЙ§AзїADЁЭyжсгкЕуDЃЌ
дк![]() жаЃЌСюy=0ПЩЧѓЕУx= -3Лђx=1ЃЌ
жаЃЌСюy=0ПЩЧѓЕУx= -3Лђx=1ЃЌ
ЁрCЃЈ-3,0ЃЉЃЌЧвAЃЈ-2ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрAC=![]()
гЩЗелЕФаджЪПЩжЊAN=AC=![]() ЃЌ
ЃЌ
ЁпЁїAMNЮЊИУХзЮяЯпЕФЁАбмЩњШ§НЧаЮЁБЃЌ
ЁрNдкyжсЩЯЃЌЧвAD=2ЃЌ
дкRtЁїANDжаЃЌгЩЙДЙЩЖЈРэПЩЕУ
DN=![]() ЃЌ
ЃЌ
ЁпOD=![]() ЃЌ
ЃЌ
ЁрON=![]() ЛђON=
ЛђON=![]() ЃЌ
ЃЌ
ЁрNЕуЕФзјБъЮЊЃЈ0ЃЌ![]() ЃЉЃЌЃЈ0ЃЌ
ЃЉЃЌЃЈ0ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
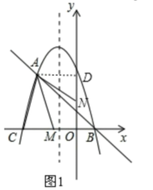
ЃЈ3ЃЉЂйЕБACЮЊЦНааЫФБпаЮЕФБпЪБЃЌШчЭМ2 ЃЌЙ§FзїЖдГЦжсЕФДЙЯпFHЃЌЙ§AзїAKЁЭxжсгкЕуKЃЌдђгаACЁЮEFЧвAC=EFЃЌ
ЁрЁЯ ACK=ЁЯ EFHЃЌ
дкЁї ACKКЭЁї EFHжа
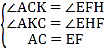
ЁрЁї ACKЁеЁї EFHЃЌ
ЁрFH=CK=1ЃЌHE=AK=![]() ЃЌ
ЃЌ
ЁпХзЮяЯпЕФЖдГЦжсЮЊx=-1ЃЌ
Ёр FЕуЕФКсзјБъЮЊ0Лђ-2ЃЌ
ЁпЕуFдкжБЯпABЩЯЃЌ
ЁрЕБFЕуЕФКсзјБъЮЊ0ЪБЃЌдђFЃЈ0ЃЌ![]() ЃЉЃЌДЫЪБЕуEдкжБЯпABЯТЗНЃЌ
ЃЉЃЌДЫЪБЕуEдкжБЯпABЯТЗНЃЌ
ЁрEЕНyжсЕФОрРыЮЊEH-OF=![]() -
-![]() =
=![]() ЃЌМДEЕФзнзјБъЮЊ-
ЃЌМДEЕФзнзјБъЮЊ-![]() ЃЌ
ЃЌ
Ёр EЃЈ-1ЃЌ-![]() ЃЉЃЛ
ЃЉЃЛ
ЕБFЕуЕФКсзјБъЮЊ-2ЪБЃЌдђFгыAжиКЯЃЌВЛКЯЬтвтЃЌЩсШЅЃЛ
ЂкЕБACЮЊЦНааЫФБпаЮЕФЖдНЧЯпЪБЃЌ
Ёп CЃЈ-3,0ЃЉЃЌЧвAЃЈ-2ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрЯпЖЮACЕФжаЕузјБъЮЊЃЈ-2.5ЃЌ ![]() ЃЉЃЌ
ЃЉЃЌ
ЩшEЃЈ-1ЃЌtЃЉЃЌFЃЈxЃЌyЃЉЃЌ
дђx-1=2ЁСЃЈ-2.5ЃЉЃЌy+t=![]() ЃЌ
ЃЌ
Ёрx= -4ЃЌy=![]() -tЃЌ
-tЃЌ
![]() -t=-
-t=-![]() ЁСЃЈ-4ЃЉ+
ЁСЃЈ-4ЃЉ+![]() ЃЌНтЕУt=
ЃЌНтЕУt=![]() ЃЌ
ЃЌ
ЁрEЃЈ-1ЃЌ![]() ЃЉЃЌFЃЈ-4ЃЌ
ЃЉЃЌFЃЈ-4ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
злЩЯПЩжЊДцдкТњзуЬѕМўЕФЕуFЃЌДЫЪБEЃЈ-1ЃЌ-![]() ЃЉЁЂЃЈ0ЃЌ
ЃЉЁЂЃЈ0ЃЌ![]() ЃЉЛђEЃЈ-1ЃЌ
ЃЉЛђEЃЈ-1ЃЌ![]() ЃЉЃЌFЃЈ-4ЃЌ
ЃЉЃЌFЃЈ-4ЃЌ![]() ЃЉ
ЃЉ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊМгПь5GЭјТчНЈЩшЃЌФГвЦЖЏЭЈаХЙЋЫОдквЛИіЦТЖШЮЊ2ЃК1ЕФЩНбќЩЯНЈСЫвЛзљ5GаХКХЭЈаХЫўABЃЌдкОрЩННХCДІЫЎЦНОрРы39УзЕФЕуDДІВтЕУЭЈаХЫўЕзBДІЕФбіНЧЪЧ35ЁуЃЌВтЕУЭЈаХЫўЖЅAДІЕФбіНЧЪЧ49ЁуЃЌ(ВЮПМЪ§ОнЃКsin35ЁуЁж0.57ЃЌtan35ЁуЁж0.70ЃЌsin49ЁуЁж0.75ЃЌtan49ЁуЁж1.15)ЃЌдђЭЈаХЫўABЕФИпЖШдМЮЊ( )
A.27УзB.31УзC.48УзD.52Уз
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃАЫФъМЖбЇЩњдквЛДЮЩфЛїбЕСЗжаЃЌЫцЛњГщШЁ10УћбЇЩњЕФГЩМЈШчЯТБэЃЌЧыЛиД№ЮЪЬтЃК
ЛЗЪ§ | 6 | 7 | 8 | 9 |
ШЫЪ§ | 1 | 5 | 2 |
ЃЈ1ЃЉЬюПеЃК10УћбЇЩњЕФЩфЛїГЩМЈЕФжкЪ§ЪЧЁЁ ЁЁЃЌжаЮЛЪ§ЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉЧѓет10УћбЇЩњЕФЦНОљГЩМЈЃЎ
ЃЈ3ЃЉШє9ЛЗЃЈКЌ9ЛЗЃЉвдЩЯЦРЮЊгХауЩфЪжЃЌЪдЙРМЦШЋФъМЖ500УћбЇЩњжагаЖрЩйЪЧгХауЩфЪжЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаНсТле§ШЗЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
ЃЈ1ЃЉвЛИіЖрБпаЮЕФФкНЧКЭЪЧЭтНЧКЭЕФ3БЖЃЌдђетИіЖрБпаЮЪЧСљБпаЮЃЛ
ЃЈ2ЃЉШчЙћвЛИіШ§НЧаЮЕФШ§БпГЄЗжБ№ЮЊ6ЁЂ8ЁЂ10ЃЌдђзюГЄБпЩЯЕФжаЯпГЄЮЊ5ЃЛ
ЃЈ3ЃЉШєЁїABCЁзЁїDEFЃЌЯрЫЦБШЮЊ1ЃК4ЃЌдђSЁїABCЃКSЁїDEF=1ЃК4ЃЛ
ЃЈ4ЃЉШєЕШбќШ§НЧаЮвЛИіНЧЮЊ80ЁуЃЌдђЕзНЧЮЊ80ЁуЛђ50ЁуЃЎ
A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕ![]() жаЃЌвЛДЮКЏЪ§
жаЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЗДБШР§КЏЪ§
ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгк
ЕФЭМЯѓНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЎ
СНЕуЃЎ
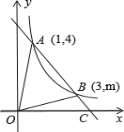
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ3ЃЉШчЭМаДГіЗДБШР§КЏЪ§жЕДѓгквЛДЮКЏЪ§жЕЕФздБфСП![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+6ОЙ§ЕуAЃЈЉ2ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЎЕуDЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЕуDЕФКсзјБъЮЊmЃЈ1ЃМmЃМ4ЃЉЃЌСЌНгACЃЌBCЃЌDBЃЌDCЃЎ
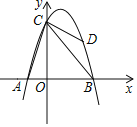
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪН.
ЃЈ2ЃЉЕБЁїBCDЕФУцЛ§ЕШгкЁїAOCЕФУцЛ§ЕФ![]() ЪБЃЌЧѓmЕФжЕ.
ЪБЃЌЧѓmЕФжЕ.
ЃЈ3ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдквЛЕуQЃЌЪЙЕУЁїQACЕФжмГЄзюаЁЃЌШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌЕуMЁЂNЗжБ№дкABЁЂBCЩЯЃЌAB=4ЃЌAM=1ЃЌBN=![]() .
.

(1)ЧѓжЄ:ІЄADMЁзІЄBMNЃЛ
(2)ЧѓЁЯDMNЕФЖШЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОаЁЬтТњЗж9ЗжЃЉ
ИљОнвЊЧѓЃЌНтД№ЯТСаЮЪЬтЃЎ
ЃЈ1ЃЉИљОнвЊЧѓЃЌНтД№ЯТСаЮЪЬтЃЎ
ЂйЗНГЬx2Ѓ2xЃЋ1ЃН0ЕФНтЮЊ________________________ЃЛ
ЂкЗНГЬx2Ѓ3xЃЋ2ЃН0ЕФНтЮЊ________________________ЃЛ
ЂлЗНГЬx2Ѓ4xЃЋ3ЃН0ЕФНтЮЊ________________________ЃЛ
ЁЁ ЁЁ
ЃЈ2ЃЉИљОнвдЩЯЗНГЬЬиеїМАЦфНтЕФЬиеїЃЌЧыВТЯыЃК
ЂйЗНГЬx2Ѓ9xЃЋ8ЃН0ЕФНтЮЊ________________________ЃЛ
ЂкЙигкxЕФЗНГЬ________________________ЕФНтЮЊx1ЃН1ЃЌx2ЃНnЃЎ
ЃЈ3ЃЉЧыгУХфЗНЗЈНтЗНГЬx2Ѓ9xЃЋ8ЃН0ЃЌвдбщжЄВТЯыНсТлЕФе§ШЗадЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
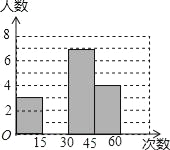
ЁОЬтФПЁПдкДѓПЮМфЛюЖЏжаЃЌЬхг§РЯЪІЫцЛњГщШЁСЫЦпФъМЖМзЁЂввСНАрВПЗжХЎбЇЩњНјаабіЮдЦ№зјЕФВтЪдЃЌВЂЖдГЩМЈНјааЭГМЦЗжЮіЃЌЛцжЦСЫЦЕЪ§ЗжВМБэКЭЭГМЦЭМЃЌЧыФуИљОнЭМБэжаЕФаХЯЂЭъГЩЯТСаЮЪЬтЃК
Зж зщ | ЦЕЪ§ | ЦЕТЪ |
ЕквЛзщЃЈ0ЁмxЃМ15ЃЉ | 3 | 0.15 |
ЕкЖўзщЃЈ15ЁмxЃМ30ЃЉ | 6 | a |
ЕкШ§зщЃЈ30ЁмxЃМ45ЃЉ | 7 | 0.35 |
ЕкЫФзщЃЈ45ЁмxЃМ60ЃЉ | b | 0.20 |
ЃЈ1ЃЉЦЕЪ§ЗжВМБэжаa=_____ЃЌb=_____ЃЌВЂНЋЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉШчЙћИУаЃЦпФъМЖЙВгаХЎЩњ180ШЫЃЌЙРМЦбіЮдЦ№зјФмЙЛвЛЗжжгЭъГЩ30Лђ30ДЮвдЩЯЕФХЎбЇЩњгаЖрЩйШЫЃП
ЃЈ3ЃЉвбжЊЕквЛзщжажЛгавЛИіМзАрбЇЩњЃЌЕкЫФзщжажЛгавЛИіввАрбЇЩњЃЌРЯЪІЫцЛњДгетСНИізщжаИїбЁвЛУћбЇЩњЬИаФЕУЬхЛсЃЌдђЫљбЁСНШЫе§КУЖМЪЧМзАрбЇЩњЕФИХТЪЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com