
【题目】如图,在正方形ABCD中,点M、N分别在AB、BC上,AB=4,AM=1,BN=![]() .
.

(1)求证:ΔADM∽ΔBMN;
(2)求∠DMN的度数.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
⑴请你补全这个输水管道的圆形截面;
⑵若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着夏季的到来,各类水果自然也成了大众喜爱的消费产品.已知某水果店第一次售出苹果和芒果共200千克,其中苹果的售价为24元/千克,芒果的售价为20元/千克,总销售额为4320元.
(1)求水果店第一次售出苹果和芒果各多少千克;
(2)通过最近的调查发现消费者更加青睐于购买芒果,经销售统计发现与第一次相比,芒果的售价每降低1元,销量就增加20千克,苹果的售价和销量均保持不变,如果第二次的苹果和芒果全部售完比第一次的总销售额多980元,求第二次芒果的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“衍生直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“衍生三角形”.已知抛物线![]() 与其“衍生直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“衍生直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.

(1)填空:该抛物线的“衍生直线”的解析式为 ,点A的坐标为 ,点B的坐标为 ;
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“衍生三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“衍生直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件30元,现在的售价为每件40元,每星期可卖出200件.市场调查反映:如果每件的售价每涨1元,那么每星期少卖10件.设每件涨价x元,每星期的销量为y件.
(1)求y与x的函数关系式;
(2)如何定价才能使每星期的利润最大且每星期的销量较大?每星期的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
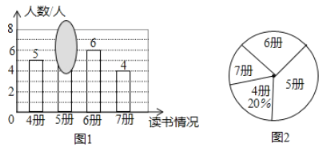
(1)求条形图中被遮盖的数,并计算册数的平均数和中位数;
(2)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了__________人.从补查结果看,学生的读书册数的平均数与之前相比______________.(变大、变小、不变).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2bx+c的图象经过点M(1,0),顶点坐标(m,n)
(1)当x<5时,y随x的增大而增大,求b的取值范围;
(2)求n关于m的函数解析式;
(3)求该二次函数的图象顶点最低时的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 为
为![]() 边的中点,以点
边的中点,以点![]() 为顶点的
为顶点的![]() 的两边分别与边
的两边分别与边![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,且
,且![]() 与
与![]() 互补.
互补.
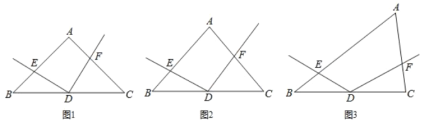
(1)如图1,若![]() ,且
,且![]() ,请直接写出:线段
,请直接写出:线段![]() 与
与![]() 的数量关系______;
的数量关系______;
(2)如图2,若![]() ,请直接写出:线段
,请直接写出:线段![]() 与
与![]() 的数量关系______;
的数量关系______;
(3)如图3,若![]() ,探索线段
,探索线段![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )
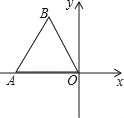
A. (2,2![]() ) B. (﹣2,4) C. (﹣2,2
) B. (﹣2,4) C. (﹣2,2![]() ) D. (﹣2,2
) D. (﹣2,2![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com