
【题目】已知二次函数y=﹣x2+2bx+c的图象经过点M(1,0),顶点坐标(m,n)
(1)当x<5时,y随x的增大而增大,求b的取值范围;
(2)求n关于m的函数解析式;
(3)求该二次函数的图象顶点最低时的解析式.
【答案】(1)b≥5;(2)n=m2﹣2m+1;(3)y=﹣x2+2x﹣1.
【解析】
(1)由二次函数y=﹣x2+2bx+c可知开口向下,求出对称轴为x=b,进而求得b的取值范围.
(2)由图象经过点M(1,0),可将M点坐标代入求出c=1﹣2b,进而利用顶点坐标公式即可求值.
(3)由n=(m﹣1)2,可求得最低点(1,0),进而代入求得函数解析式.
解:(1)由二次函数y=﹣x2+2bx+c可知开口向下,对称轴为直线x=b,
∵当x<5时,y随x的增大而增大,
∴b≥5;
(2)∵二次函数y=﹣x2+2bx+c的图象经过点M(1,0),
∴﹣1+2b+c=0,
∴c=1﹣2b,
∵m=b,n=![]() =c+b2=1﹣2b+b2,
=c+b2=1﹣2b+b2,
∴n=m2﹣2m+1;
(3)∵n=(m﹣1)2,
∴顶点有最低点(1,0),
∵a=﹣1,
∴二次函数的解析式为y=﹣(x﹣1)2=﹣x2+2x﹣1.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
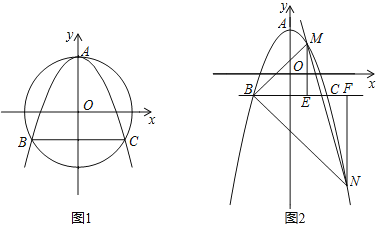
【题目】已知抛物线y=ax2+bx+c过顶点A(0,2),以原点O为圆心,OA为半径的圆与抛物线的另两个交点为B,C,且B在C的左侧,△ABC有一个内角为60°.
(1)求抛物线的解析式.
(2)若MN与直线y=﹣2![]() x平行,M(x1,y1),N(x2,y2),M,N都在抛物线上,且M,N位于直线BC的两侧,y1>y2,ME⊥BC于E,NF⊥BC于F,解决以下问题:
x平行,M(x1,y1),N(x2,y2),M,N都在抛物线上,且M,N位于直线BC的两侧,y1>y2,ME⊥BC于E,NF⊥BC于F,解决以下问题:
①求证:![]() .
.
②求△MBC外心的纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
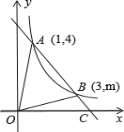
(1)求反比例函数的解析式;
(2)求![]() 的面积;
的面积;
(3)如图写出反比例函数值大于一次函数值的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经销的太阳路灯,标价为4000元/个,促销活动期间,其优惠方法如下:
A.一次性购买数量不超过80个,按标价收费;
B.一次性购买数量超过80个,每多买一个,所购路灯每个可降价8元,但单价最低不能低于3200元/个.
(1)购买80个这样的路灯,应需付款_________________元.
(2)若一顾客一次性购买这样的路灯用去516000元,则该顾客实际购买了多少个这样的路灯.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)
根据要求,解答下列问题.
(1)根据要求,解答下列问题.
①方程x2-2x+1=0的解为________________________;
②方程x2-3x+2=0的解为________________________;
③方程x2-4x+3=0的解为________________________;
…… ……
(2)根据以上方程特征及其解的特征,请猜想:
①方程x2-9x+8=0的解为________________________;
②关于x的方程________________________的解为x1=1,x2=n.
(3)请用配方法解方程x2-9x+8=0,以验证猜想结论的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
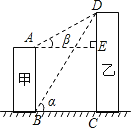
【题目】如图,线段AB、DC分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,从B点测得D点的仰角α为60°从A点测得D点的仰角β为30°,已知甲建筑物高AB=36米.
(1)求乙建筑物的高DC;
(2)求甲、乙两建筑物之间的距离BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上(不与端点重合),
上(不与端点重合),![]() ,射线
,射线![]() 交
交![]() 延长线于点
延长线于点![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() .
.
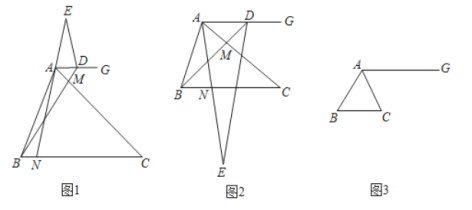
(1)(观察猜想)如图1,点![]() 在射线
在射线![]() 上,当
上,当![]() 时,
时,
①线段![]() 与
与![]() 的数量关系是______;
的数量关系是______;
②![]() 的度数是______;
的度数是______;
(2)(探究证明)如图2点![]() 在射线
在射线![]() 上,当
上,当![]() 时,判断并证明线段
时,判断并证明线段![]() 与
与![]() 的数量关系,求
的数量关系,求![]() 的度数;
的度数;
(3)(拓展延伸)如图3,点![]() 在直线
在直线![]() 上,当
上,当![]() 时,
时,![]() ,点
,点![]() 是
是![]() 边上的三等分点,直线
边上的三等分点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com