
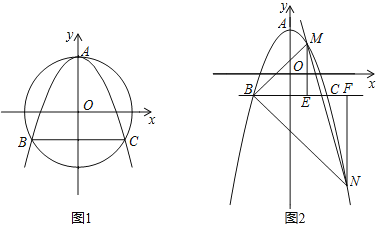
【题目】已知抛物线y=ax2+bx+c过顶点A(0,2),以原点O为圆心,OA为半径的圆与抛物线的另两个交点为B,C,且B在C的左侧,△ABC有一个内角为60°.
(1)求抛物线的解析式.
(2)若MN与直线y=﹣2![]() x平行,M(x1,y1),N(x2,y2),M,N都在抛物线上,且M,N位于直线BC的两侧,y1>y2,ME⊥BC于E,NF⊥BC于F,解决以下问题:
x平行,M(x1,y1),N(x2,y2),M,N都在抛物线上,且M,N位于直线BC的两侧,y1>y2,ME⊥BC于E,NF⊥BC于F,解决以下问题:
①求证:![]() .
.
②求△MBC外心的纵坐标的取值范围.
【答案】(1)抛物线解析式为y=﹣x2+2;(2)①证明见解析;②﹣![]() <y0≤0.
<y0≤0.
【解析】
(1)由顶点坐标为(0,2)可得c=2,由对称轴为y轴可得b=0,△ABC为等腰三角形,根据有一个角是60°可得△ABC是等边三角形,设线段BC与y轴的交点为点D,连接OB,根据垂径定理可得BD=CD,根据外心的定义可得∠OBD=30°,利用∠OBD的正弦和余弦值可求出OD和BD的长,即可得得B坐标,代入抛物线解析式可求出a值,即可得答案;(2)①根据MN与y=﹣2![]() x平行设直线MN的解析式为y=﹣2
x平行设直线MN的解析式为y=﹣2![]() x+m,把M点坐标代入可得m=﹣x12+2
x+m,把M点坐标代入可得m=﹣x12+2![]() x1+2,即可得出MN的解析式,代入y=﹣x2+2可用x1表示出x2,进而可表示出y2,分别用x1表示出∠MBE和∠NBF的正切函数即可得结论;②过M作ME⊥y轴于E,由y轴为BC的垂直平分线,可知△NBC的外心在y轴上,设外心P坐标为(0,y0),可得PB=PM,利用勾股定理可用y1表示出y0,根据y1的取值范围即可得答案.
x1+2,即可得出MN的解析式,代入y=﹣x2+2可用x1表示出x2,进而可表示出y2,分别用x1表示出∠MBE和∠NBF的正切函数即可得结论;②过M作ME⊥y轴于E,由y轴为BC的垂直平分线,可知△NBC的外心在y轴上,设外心P坐标为(0,y0),可得PB=PM,利用勾股定理可用y1表示出y0,根据y1的取值范围即可得答案.
(1)∵抛物线过点A(0,2),
∴c=2,
∴抛物线的对称轴为y轴,且开口向下,即b=0,
∵以O为圆心,OA为半径的圆与抛物线交于另两点B,C,y轴为抛物线对称轴,
∴B、C关于y轴对称,
∴△ABC为等腰三角形,
∵△ABC中有一个角为60°,
∴△ABC为等边三角形,且OC=OA=2,
设线段BC与y轴的交点为点D,连接OB,
∵AD⊥BC,AD过圆心,
∴BD=CD,
∵O为△ABC的外心,△ABC为等边三角形,
∴∠OBD=30°,
∴BD=OBcos30°=![]() ,OD=OBsin30°=1,
,OD=OBsin30°=1,
∵B在C的左侧,
∴B的坐标为(﹣![]() ,﹣1),
,﹣1),
∵B点在抛物线上,且c=2,b=0,
∴3a+2=﹣1,
解得:a=﹣1,
则抛物线解析式为y=﹣x2+2.
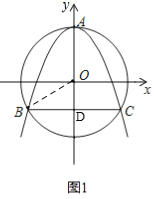
(2)①由(1)知,点M(x1,﹣x12+2),N(x2,﹣x22+2),
∵MN与直线y=﹣2![]() x平行,
x平行,
∴设直线MN的解析式为y=﹣2![]() x+m,
x+m,
∴﹣x12+2=﹣2![]() x1+m,即m=﹣x12+2
x1+m,即m=﹣x12+2![]() x1+2,
x1+2,
∴直线MN解析式为y=﹣2![]() x﹣x12+2
x﹣x12+2![]() x1+2,
x1+2,
把y=﹣2![]() x﹣x12+2
x﹣x12+2![]() x1+2代入y=﹣x2+2,
x1+2代入y=﹣x2+2,
解得:x=x1或x=2![]() ﹣x1,
﹣x1,
∴x2=2![]() ﹣x1,即y2=﹣(2
﹣x1,即y2=﹣(2![]() ﹣x1)2+2=﹣x12+4
﹣x1)2+2=﹣x12+4![]() x1﹣10,
x1﹣10,
如图2所示,作ME⊥BC,NF⊥BC,垂足为E,F,
∵M,N位于直线BC的两侧,且y1>y2,
∴y2<﹣1<y1≤2,且﹣![]() <x1<x2,
<x1<x2,
∴ME=y1﹣(﹣1)=﹣x12+3,BE=x1﹣(﹣![]() )=x1+
)=x1+![]() ,
,
NF=﹣1﹣y2=x12﹣4![]() x1+9,BF=x2﹣(﹣
x1+9,BF=x2﹣(﹣![]() )=3
)=3![]() ﹣x1,
﹣x1,
在Rt△BEM中,tan∠MBE=![]() =
=![]() =
=![]() ﹣x1,
﹣x1,
在Rt△BFN中,tan∠NBF=![]() =
=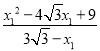
=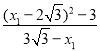
=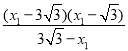
=![]() -x1,
-x1,
∴![]() =
=![]() .
.
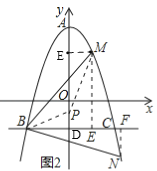
②过M作ME⊥y轴于E,
∵y轴为BC的垂直平分线,
∴设△MBC的外心为P(0,y0),则PB=PM,即PB2=PM2,
∵B的坐标为(﹣![]() ,﹣1),
,﹣1),
∴PD=y0+1,PD=![]() ,ME=x1,PE=y1﹣y0,
,ME=x1,PE=y1﹣y0,
根据勾股定理得:3+(y0+1)2=x12+(y1﹣y0)2,
∵x12=2﹣y1,
∴y02+2y0+4=(2﹣y1)+(y0﹣y1)2,即y0=![]() y1﹣1,
y1﹣1,
由①得:﹣1<y1≤2,
∴﹣![]() <y0≤0,
<y0≤0,
则△MBC的外心的纵坐标的取值范围是﹣![]() <y0≤0.
<y0≤0.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交与A(1,0),B(﹣3,0)两点,顶点为D,交y轴于C.
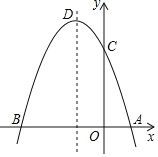
(1)求该抛物线的解析式.
(2)在抛物线的对称轴上是否存在着一点M使得MA+MC的值最小,若存在求出M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
⑴请你补全这个输水管道的圆形截面;
⑵若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
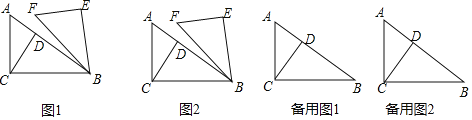
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 于点D,将
于点D,将![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() 得到
得到![]()
![]() 如图2,当
如图2,当![]() 时,求点C、E之间的距离;
时,求点C、E之间的距离;
![]() 在旋转过程中,当点A、E、F三点共线时,求AF的长;
在旋转过程中,当点A、E、F三点共线时,求AF的长;
![]() 连结AF,记AF的中点为P,请直接写出线段CP长度的最小值.
连结AF,记AF的中点为P,请直接写出线段CP长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=10.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边经过点C,另一直角边AB交于点E.
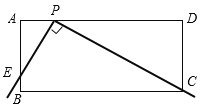
(1)求证:![]()
(2)是否存在这样的点P,使![]() 的周长等于
的周长等于![]() 周长的2倍?若存在,求出DP的长;若不存在,请说明理由.
周长的2倍?若存在,求出DP的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着夏季的到来,各类水果自然也成了大众喜爱的消费产品.已知某水果店第一次售出苹果和芒果共200千克,其中苹果的售价为24元/千克,芒果的售价为20元/千克,总销售额为4320元.
(1)求水果店第一次售出苹果和芒果各多少千克;
(2)通过最近的调查发现消费者更加青睐于购买芒果,经销售统计发现与第一次相比,芒果的售价每降低1元,销量就增加20千克,苹果的售价和销量均保持不变,如果第二次的苹果和芒果全部售完比第一次的总销售额多980元,求第二次芒果的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2bx+c的图象经过点M(1,0),顶点坐标(m,n)
(1)当x<5时,y随x的增大而增大,求b的取值范围;
(2)求n关于m的函数解析式;
(3)求该二次函数的图象顶点最低时的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com