
【题目】如图,在直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
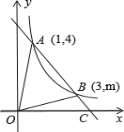
(1)求反比例函数的解析式;
(2)求![]() 的面积;
的面积;
(3)如图写出反比例函数值大于一次函数值的自变量![]() 的取值范围.
的取值范围.
科目:初中数学 来源: 题型:
【题目】为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着夏季的到来,各类水果自然也成了大众喜爱的消费产品.已知某水果店第一次售出苹果和芒果共200千克,其中苹果的售价为24元/千克,芒果的售价为20元/千克,总销售额为4320元.
(1)求水果店第一次售出苹果和芒果各多少千克;
(2)通过最近的调查发现消费者更加青睐于购买芒果,经销售统计发现与第一次相比,芒果的售价每降低1元,销量就增加20千克,苹果的售价和销量均保持不变,如果第二次的苹果和芒果全部售完比第一次的总销售额多980元,求第二次芒果的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“衍生直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“衍生三角形”.已知抛物线![]() 与其“衍生直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“衍生直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.

(1)填空:该抛物线的“衍生直线”的解析式为 ,点A的坐标为 ,点B的坐标为 ;
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“衍生三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“衍生直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件30元,现在的售价为每件40元,每星期可卖出200件.市场调查反映:如果每件的售价每涨1元,那么每星期少卖10件.设每件涨价x元,每星期的销量为y件.
(1)求y与x的函数关系式;
(2)如何定价才能使每星期的利润最大且每星期的销量较大?每星期的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2bx+c的图象经过点M(1,0),顶点坐标(m,n)
(1)当x<5时,y随x的增大而增大,求b的取值范围;
(2)求n关于m的函数解析式;
(3)求该二次函数的图象顶点最低时的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,关于点![]() 的图象变化有以下说法:
的图象变化有以下说法:
①点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 的坐标为
的坐标为![]()
②点![]() 与点
与点![]() 关于原点对称
关于原点对称
③把点![]() 先向右平移
先向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度得到点
个单位长度得到点![]()
④把点![]() 绕原点顺时针旋转
绕原点顺时针旋转![]() ,得到点
,得到点![]()
其中,正确的说法是( )
A. ①③④ B. ①②③④ C. ①②③ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com