
【题目】已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上(不与端点重合),
上(不与端点重合),![]() ,射线
,射线![]() 交
交![]() 延长线于点
延长线于点![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() .
.
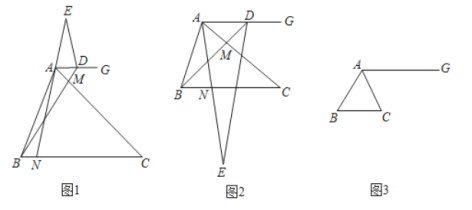
(1)(观察猜想)如图1,点![]() 在射线
在射线![]() 上,当
上,当![]() 时,
时,
①线段![]() 与
与![]() 的数量关系是______;
的数量关系是______;
②![]() 的度数是______;
的度数是______;
(2)(探究证明)如图2点![]() 在射线
在射线![]() 上,当
上,当![]() 时,判断并证明线段
时,判断并证明线段![]() 与
与![]() 的数量关系,求
的数量关系,求![]() 的度数;
的度数;
(3)(拓展延伸)如图3,点![]() 在直线
在直线![]() 上,当
上,当![]() 时,
时,![]() ,点
,点![]() 是
是![]() 边上的三等分点,直线
边上的三等分点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.
【答案】(1)①![]() ,②
,②![]() ;(2)
;(2)![]() ;(3)满足条件的
;(3)满足条件的![]() 的长为
的长为![]() 或4.
或4.
【解析】
(1)①延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点O,先由等边对等角得到
于点O,先由等边对等角得到![]() ,然后证明
,然后证明![]() ,即可得到BM=AN;②再由等边对等角和平行线推出
,即可得到BM=AN;②再由等边对等角和平行线推出![]() ,由三角形外角性质得到
,由三角形外角性质得到![]() ,可推出
,可推出![]() ,即可得
,即可得![]() .
.
(2)同理可证![]() ,同(1)可推出
,同(1)可推出 ![]() ,最后得到
,最后得到![]() .
.
(3)当![]() 时,作
时,作![]() 于
于![]() ,在
,在![]() 中,利用60°可求出边长,然后在在
中,利用60°可求出边长,然后在在![]() 中求出BM,再由
中求出BM,再由![]() ,利用相似比求出CF,当
,利用相似比求出CF,当![]() 时,同法可求
时,同法可求![]() .
.
(1)①如图1中,延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点O.
于点O.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
②∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵∠ANB+∠ENF=180°,∠BMA+∠BMC=180°,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为①![]() ,②
,②![]() .
.
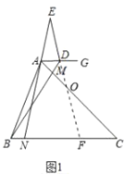
(2)如图2中,设![]() 交
交![]() 于点
于点![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
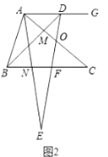
(3)①如图3-1中,当![]() 时,作
时,作![]() 于
于![]() .
.
由题意![]() ,在
,在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,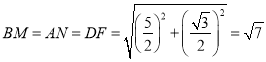 ,
,
由(2)可知:![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
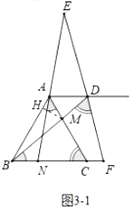
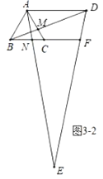
②如图3-2中,当![]() 时,同法可得
时,同法可得![]() .
.
综上所述,满足条件的![]() 的长为
的长为![]() 或4.
或4.


科目:初中数学 来源: 题型:
【题目】随着夏季的到来,各类水果自然也成了大众喜爱的消费产品.已知某水果店第一次售出苹果和芒果共200千克,其中苹果的售价为24元/千克,芒果的售价为20元/千克,总销售额为4320元.
(1)求水果店第一次售出苹果和芒果各多少千克;
(2)通过最近的调查发现消费者更加青睐于购买芒果,经销售统计发现与第一次相比,芒果的售价每降低1元,销量就增加20千克,苹果的售价和销量均保持不变,如果第二次的苹果和芒果全部售完比第一次的总销售额多980元,求第二次芒果的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2bx+c的图象经过点M(1,0),顶点坐标(m,n)
(1)当x<5时,y随x的增大而增大,求b的取值范围;
(2)求n关于m的函数解析式;
(3)求该二次函数的图象顶点最低时的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 为
为![]() 边的中点,以点
边的中点,以点![]() 为顶点的
为顶点的![]() 的两边分别与边
的两边分别与边![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,且
,且![]() 与
与![]() 互补.
互补.
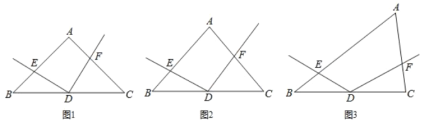
(1)如图1,若![]() ,且
,且![]() ,请直接写出:线段
,请直接写出:线段![]() 与
与![]() 的数量关系______;
的数量关系______;
(2)如图2,若![]() ,请直接写出:线段
,请直接写出:线段![]() 与
与![]() 的数量关系______;
的数量关系______;
(3)如图3,若![]() ,探索线段
,探索线段![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
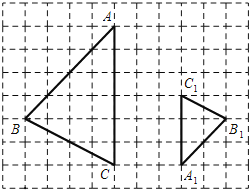
【题目】如图,在![]() 网格图中,
网格图中,![]() 与
与![]() 是位似图形.
是位似图形.
![]() 若在网格上建立平面直角坐标系,使得点A的坐标为
若在网格上建立平面直角坐标系,使得点A的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,写出点B的坐标;
,写出点B的坐标;
![]() 以点A为位似中心,在网格图中作
以点A为位似中心,在网格图中作![]() ,使
,使![]() 和
和![]() 位似,且位似比为1:2;
位似,且位似比为1:2;
![]() 在图上标出
在图上标出![]() 与
与![]() 的位似中心P,并写出点P的坐标,计算四边形ABCP的周长.
的位似中心P,并写出点P的坐标,计算四边形ABCP的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
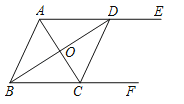
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADB=30°,BD=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,关于点![]() 的图象变化有以下说法:
的图象变化有以下说法:
①点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 的坐标为
的坐标为![]()
②点![]() 与点
与点![]() 关于原点对称
关于原点对称
③把点![]() 先向右平移
先向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度得到点
个单位长度得到点![]()
④把点![]() 绕原点顺时针旋转
绕原点顺时针旋转![]() ,得到点
,得到点![]()
其中,正确的说法是( )
A. ①③④ B. ①②③④ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
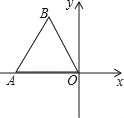
【题目】如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )
A. (2,2![]() ) B. (﹣2,4) C. (﹣2,2
) B. (﹣2,4) C. (﹣2,2![]() ) D. (﹣2,2
) D. (﹣2,2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
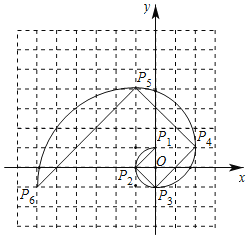
【题目】我们把1,1,2,3,5,8,13,21,…组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧,弧P1P2,弧P2P3,弧P3P4,…得到斐波那契螺旋线,然后依次连接P1P2,P2P3,P3P4得到螺旋折线(如图),已知点P1(0,1),P2(﹣1,0),P3(0,﹣1),则该折线上P10的点的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com