
【题目】如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0),与y轴交于点C.点D是抛物线上的一个动点,点D的横坐标为m(1<m<4),连接AC,BC,DB,DC.
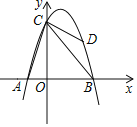
(1)求抛物线的解析式.
(2)当△BCD的面积等于△AOC的面积的![]() 时,求m的值.
时,求m的值.
(3)在抛物线的对称轴上是否存在一点Q,使得△QAC的周长最小,若存在,求出点Q的坐标.
【答案】(1)![]() ;(2)m=3;(3)点Q的坐标为(1,
;(2)m=3;(3)点Q的坐标为(1,![]() ).
).
【解析】
(1)由A、B两点坐标可得抛物线两点式解析式,进而可求出a值,即可得答案;(2)设直线BC的表达式为y=kx+b,根据抛物线的解析式可得C点坐标,利用待定系数法可得直线BC的解析式,设点D(m,![]() ),过点D作y轴的平行线交直线BC与点H,可得点H(m,
),过点D作y轴的平行线交直线BC与点H,可得点H(m,![]() ),根据三角形面积公式列方程求出m的值即可;(3)根据二次函数的对称性可得抛物线
),根据三角形面积公式列方程求出m的值即可;(3)根据二次函数的对称性可得抛物线![]() 的轴对称与BC的交点即为点Q,根据二次函数解析式可得对称轴方程,把对称轴方程代入BC解析式即可求出Q点纵坐标,即可得答案.
的轴对称与BC的交点即为点Q,根据二次函数解析式可得对称轴方程,把对称轴方程代入BC解析式即可求出Q点纵坐标,即可得答案.
(1)∵抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0),
∴抛物线解析式为:y=a(x+2)(x﹣4)=a(x2﹣2x﹣8)=ax2﹣2ax﹣8a,
∴﹣8a=6,
解得:![]() ,
,
故抛物线的表达式为:![]() ;
;
(2)设直线BC的表达式为y=kx+b,
∵抛物线与y轴交于点C,
∴点C(0,6),
将点B、C的坐标代入一次函数表达式得:![]() ,
,
解得: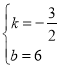 ,
,
∴直线BC的表达式为:![]() ,
,
如图1,过点D作y轴的平行线交直线BC与点H,
设点D(m,![]() ),则点H(m,
),则点H(m,![]() )
)
S△BDC=![]() HD×OB=2(
HD×OB=2(![]() )=2(
)=2(![]() ),
),
![]() S△ACO=
S△ACO=![]() ×
×![]() ×6×2=
×6×2=![]() ,
,
∴2(﹣![]() m2+3m)=
m2+3m)=![]() ,
,
解得:m=3或m=1(舍去),
∴m=3;

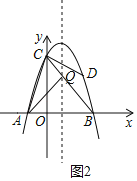
(3)如图2,在抛物线的对称轴上存在一点Q,使得△QAC的周长最小,连接BC,
∵A、B两点关于对称轴对称,
∴QA=QB,
∴QA+QC=QC+QB,
∴BC为QA+QC的最小值,即△QAC的周长最小.
∴抛物线![]() 的轴对称与BC的交点即为点Q,
的轴对称与BC的交点即为点Q,
∵抛物线![]() 的轴对称为x=1,
的轴对称为x=1,
∴把x=1代入直线BC的表达式![]() 得
得![]() ,
,
∴点Q的坐标为(1,![]() ).
).


科目:初中数学 来源: 题型:
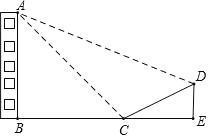
【题目】我校兴趣小组同学为测量校外“御墅临枫”的一栋电梯高层AB的楼高,从校前广场的C处测得该座建筑物顶点A的仰角为45°,沿着C向上走到30![]() 米处的D点.再测得顶点A的仰角为22°,已知CD的坡度:i=1:2,A、B、C、D在同一平面内,则高楼AB的高度为( )(参考数据;sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
米处的D点.再测得顶点A的仰角为22°,已知CD的坡度:i=1:2,A、B、C、D在同一平面内,则高楼AB的高度为( )(参考数据;sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
A.60B.70C.80D.90
查看答案和解析>>
科目:初中数学 来源: 题型:
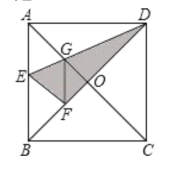
【题目】如图,在正方形纸片![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,折叠正方形纸片
,折叠正方形纸片![]() ,使
,使![]() 落在
落在![]() 上,点
上,点![]() 恰好与
恰好与![]() 上的点
上的点![]() 重合,展开后,折痕
重合,展开后,折痕![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是菱形;⑤
是菱形;⑤![]() ,其中正确结论的序号是______.
,其中正确结论的序号是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“衍生直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“衍生三角形”.已知抛物线![]() 与其“衍生直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“衍生直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.

(1)填空:该抛物线的“衍生直线”的解析式为 ,点A的坐标为 ,点B的坐标为 ;
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“衍生三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“衍生直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
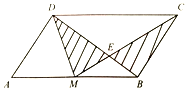
【题目】如图,M是平行四边形ABCD的AB边的中点,CM与BD相交于点E,设平行四边形ABCD的面积为1,则图中阴影部分的面积是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
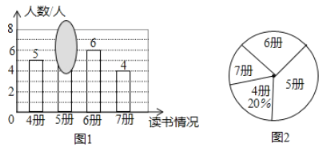
(1)求条形图中被遮盖的数,并计算册数的平均数和中位数;
(2)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了__________人.从补查结果看,学生的读书册数的平均数与之前相比______________.(变大、变小、不变).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某货车销售公司,分别试销售两种型号货车各一个月,并从中选择一种长期销售,设每月销售量为x辆若销售甲型货车,每月销售的利润为y1(万元),已知每辆甲型货车的利润为(m+6)万元,(m是常数,9≤m≤11),每月还需支出其他费用8万元,受条件限制每月最多能销售甲型货车25辆;若销售乙型货车,每月的利润y2(万元)与x的函数关系式为y2=ax2+bx-25,且当x=10时,y2=20,当x=20时,y2=55,受条件限制每月最多能销售乙型货车40辆.
(1)分别求出y1、y2与x的函数关系式,并确定x的取值范范围;
(2)分别求出销售这两种货车的最大月利润;(最大利润能求值的求值,不能求值的用式子表示)
(3)为获得最大月利润,该公司应该选择销售哪种货车?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学积极组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:

(1)求出x的值,并将不完整的条形统计图补充完整;
(2)若该校共有学生2500人,试估计每周课外阅读时间量满足2≤t<4的人数;
(3)若本次调查活动中,九年级(1)班的两个学习小组分别有3人和2人每周阅读时间量都在4小时以上,现从这5人中任选2人参加学校组织的知识抢答赛,求选出的2人来自不同小组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com