
【题目】如图,在正方形纸片![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,折叠正方形纸片
,折叠正方形纸片![]() ,使
,使![]() 落在
落在![]() 上,点
上,点![]() 恰好与
恰好与![]() 上的点
上的点![]() 重合,展开后,折痕
重合,展开后,折痕![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是菱形;⑤
是菱形;⑤![]() ,其中正确结论的序号是______.
,其中正确结论的序号是______.
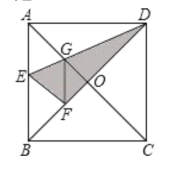
【答案】①④⑤.
【解析】
①由四边形ABCD是正方形,可得∠GAD=∠ADO=45°,又由折叠的性质,可求得∠ADG的度数;
②由AE=EF<BE,可得AD>2AE;
③由AG=GF>OG,可得△AGD的面积>△OGD的面积;
④由折叠的性质与平行线的性质,易得△EFG是等腰三角形,即可证得AE=GF;
⑤易证得四边形AEFG是菱形,由等腰直角三角形的性质,即可得BE=2OG.
∵四边形ABCD是正方形,
∴∠GAD=∠ADO=45°,
由折叠的性质可得:∠ADG=![]() ∠ADO=22.5°,得到
∠ADO=22.5°,得到![]()
故①正确.
∵由折叠的性质可得:AE=EF,∠EFD=∠EAD=90°,
∴AE=EF<BE,
∴AE<![]() AB,
AB,
∴![]() >2,
>2,
∴AD>2AE,故②错误.
∵∠AOB=90°,
∴AG=FG>OG,△AGD与△OGD同高,
∴S△AGD>S△OGD,
故③错误.
∵∠EFD=∠AOF=90°,
∴EF∥AC,
∴∠FEG=∠AGE,
∵∠AGE=∠FGE,
∴∠FEG=∠FGE,
∴EF=GF,
∵AE=EF,
∴AE=GF,
故④正确,
∵AE=EF=GF,AG=GF,
∴AE=EF=GF=AG,
∴四边形AEFG是菱形,
∴∠OGF=∠OAB=45°,
∴EF=GF=![]() OG,
OG,
∴BE=![]() EF=
EF=![]() ×
×![]() OG=2OG.
OG=2OG.
故⑤正确.
故答案为:①④⑤.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,AC与⊙O交于D,OE∥BD交⊙O于E.
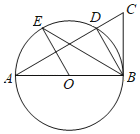
(1)求证:BE平分∠ABD.
(2)当∠A=∠E,BC=2时,求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA∶AB=1∶2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
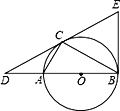
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技公司推出一款新的电子产品,该产品有三种型号.通过市场调研后,按三种型号受消费者喜爱的程度分别对A型、B型、C型产品在成本的基础上分别加价20%,30%,45%出售(三种型号的成本相同).经过一个季度的经营后,发现C型产品的销量占总销量的![]() ,且三种型号的总利润率为35%.第二个季度,公司决定对A型产品进行升级,升级后A产品的成本提高了25%,销量提高了20%;B、C产品的销量和成本均不变,且三种产品在二季度成本基础上分别加价20%,30%,45%出售,则第二个季度的总利润率为______.
,且三种型号的总利润率为35%.第二个季度,公司决定对A型产品进行升级,升级后A产品的成本提高了25%,销量提高了20%;B、C产品的销量和成本均不变,且三种产品在二季度成本基础上分别加价20%,30%,45%出售,则第二个季度的总利润率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论正确的个数是( )
(1)一个多边形的内角和是外角和的3倍,则这个多边形是六边形;
(2)如果一个三角形的三边长分别为6、8、10,则最长边上的中线长为5;
(3)若△ABC∽△DEF,相似比为1:4,则S△ABC:S△DEF=1:4;
(4)若等腰三角形一个角为80°,则底角为80°或50°.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0),与y轴交于点C.点D是抛物线上的一个动点,点D的横坐标为m(1<m<4),连接AC,BC,DB,DC.
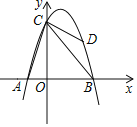
(1)求抛物线的解析式.
(2)当△BCD的面积等于△AOC的面积的![]() 时,求m的值.
时,求m的值.
(3)在抛物线的对称轴上是否存在一点Q,使得△QAC的周长最小,若存在,求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂生产一种半成品食材,成本为2元/千克,每天的产量![]() (百千克)与销售价格
(百千克)与销售价格![]() (元/千克)满足函数关系式
(元/千克)满足函数关系式![]() ,从市场反馈的信息发现,该半成品食材每天的市场需求量
,从市场反馈的信息发现,该半成品食材每天的市场需求量![]() (百千克)与销售价格
(百千克)与销售价格![]() (元/千克)满足一次函数关系,部分数据如表:
(元/千克)满足一次函数关系,部分数据如表:
销售价格 | 2 | 4 | …… | 10 |
市场需求量 | 12 | 10 | …… | 4 |
已知按物价部门规定销售价格![]() 不低于2元/千克且不高于10元/千克.
不低于2元/千克且不高于10元/千克.
(1)直接写出![]() 与
与![]() 的函数关系式,并注明自变量
的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(2)当每天的产量小于或等于市场需求量时,这种半成品食材能全部售出,而当每天的产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃.
①当每天的半成品食材能全部售出时,求![]() 的取值范围;
的取值范围;
②求厂家每天获得的利润y(百元)与销售价格![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,当![]() 为______元/千克时,利润
为______元/千克时,利润![]() 有最大值;若要使每天的利润不低于24(百元),并尽可能地减少半成品食材的浪费,则
有最大值;若要使每天的利润不低于24(百元),并尽可能地减少半成品食材的浪费,则![]() 应定为______元/千克.
应定为______元/千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮用6张背面完全相同的纸牌进行摸牌游戏,游戏规则如下:将牌面分别标有数字1、3、6的三张纸牌给小明,将牌面分别标有数字2、4、5的三张纸牌给小亮,小明小亮分别将纸牌背面朝上,从各自的三张纸牌中随机抽出一张,并将抽出的两张卡片上的数字相加,如果和为偶数,则小明获胜;如果和为奇数,则小亮获胜.
(1)小明抽到标有数字6的纸牌的概率为 ;
(2)请用树状图或列表的方法求小亮获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com