
����Ŀ��ijʳƷ������һ�ְ��Ʒʳ�ģ��ɱ�Ϊ2Ԫ/ǧ�ˣ�ÿ��IJ���![]() ����ǧ�ˣ������ۼ۸�
����ǧ�ˣ������ۼ۸�![]() ��Ԫ/ǧ�ˣ����㺯����ϵʽ
��Ԫ/ǧ�ˣ����㺯����ϵʽ![]() �����г���������Ϣ���֣��ð��Ʒʳ��ÿ����г�������
�����г���������Ϣ���֣��ð��Ʒʳ��ÿ����г�������![]() ����ǧ�ˣ������ۼ۸�
����ǧ�ˣ������ۼ۸�![]() ��Ԫ/ǧ�ˣ�����һ�κ�����ϵ���������������
��Ԫ/ǧ�ˣ�����һ�κ�����ϵ���������������
���ۼ۸� | 2 | 4 | ���� | 10 |
������� | 12 | 10 | ���� | 4 |
��֪����۲��Ź涨���ۼ۸�![]() ������2Ԫ/ǧ���Ҳ�����10Ԫ/ǧ�ˣ�
������2Ԫ/ǧ���Ҳ�����10Ԫ/ǧ�ˣ�
��1��ֱ��д��![]() ��
��![]() �ĺ�����ϵʽ����ע���Ա���
�ĺ�����ϵʽ����ע���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����ÿ��IJ���С�ڻ�����г�������ʱ�����ְ��Ʒʳ����ȫ���۳�������ÿ��IJ��������г�������ʱ��ֻ���۳������г��������İ��Ʒʳ�ģ�ʣ���ʳ�����ڱ����ڶ̶�ֻ�ܷ�����
�ٵ�ÿ��İ��Ʒʳ����ȫ���۳�ʱ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����ÿ���õ�����y����Ԫ�������ۼ۸�![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3���ڣ�2���������£���![]() Ϊ______Ԫ/ǧ��ʱ������
Ϊ______Ԫ/ǧ��ʱ������![]() �����ֵ����Ҫʹÿ���������24����Ԫ�����������ܵؼ��ٰ��Ʒʳ�ĵ��˷ѣ���
�����ֵ����Ҫʹÿ���������24����Ԫ�����������ܵؼ��ٰ��Ʒʳ�ĵ��˷ѣ���![]() Ӧ��Ϊ______Ԫ/ǧ�ˣ�
Ӧ��Ϊ______Ԫ/ǧ�ˣ�
���𰸡���1��![]() ������
������![]() ����2��
����2��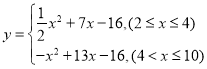 ����3��
����3��![]() ��5
��5
��������
(1)��![]() ��
��![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��![]() �����ݱ����е��������ô���ϵ����������⼴�ɣ�
�����ݱ����е��������ô���ϵ����������⼴�ɣ�
(2)����ÿ��İ��Ʒʳ����ȫ���۳�ʱ����![]() ���ݴ��в���ʽ������⼴�ɣ�
���ݴ��в���ʽ������⼴�ɣ�
�������Ա���Ϊ![]() ��
��![]() ��������ֱ���ʽ������⼴�ɣ�
��������ֱ���ʽ������⼴�ɣ�
(3)����(2)�е�������ö��κ��������ʷֱ�������ۼ�����ô�.
(1)�ɱ�������ݣ���![]() ��
��![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��![]() ��
��
���ݱ�������ݵ�![]() �����
�����![]() ��
��
��![]() ��
��![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��![]() ������
������![]() ��
��
(2)����ÿ��İ��Ʒʳ����ȫ���۳�ʱ����![]() ��
��
��![]() �����
�����![]() ��
��
��![]() �����Դ�ʱ
�����Դ�ʱ![]() ��
��
��������֪����![]() ʱ��
ʱ��
![]() ��
��
��![]() ʱ��
ʱ��![]()
![]()
![]() ��
��
����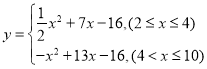 ��
��
(3)��![]() ʱ��
ʱ��
![]() �ĶԳ���Ϊ
�ĶԳ���Ϊ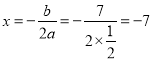 ��
��
����![]() ʱ��y����x�����������
ʱ��y����x�����������
��![]() ʱ�����ֵ��
ʱ�����ֵ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ʱȡ���ֵ��
ʱȡ���ֵ��
����ʱ![]() ���������
���������
Ҫʹÿ���������24��Ԫ����![]() ʱ����Ȼ�����ϣ�
ʱ����Ȼ�����ϣ�
��![]() �����
�����![]() ��
��
�ʵ�![]() ʱ���ܱ�֤������24��Ԫ��
ʱ���ܱ�֤������24��Ԫ��
�ʴ�Ϊ��![]() ��5.
��5.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��������![]() �Գ����ϵ�һ�㣬����OA����AΪ��ת���Ľ�AO��ʱ����ת90��õ�AO�䣬��O��ǡ��������������ʱ����A������Ϊ______________��
�Գ����ϵ�һ�㣬����OA����AΪ��ת���Ľ�AO��ʱ����ת90��õ�AO�䣬��O��ǡ��������������ʱ����A������Ϊ______________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
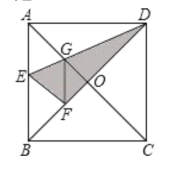
����Ŀ����ͼ����������ֽƬ![]() �У��Խ���
�У��Խ���![]() ��
��![]() ���ڵ�
���ڵ�![]() ���۵�������ֽƬ
���۵�������ֽƬ![]() ��ʹ
��ʹ![]() ����
����![]() �ϣ���
�ϣ���![]() ǡ����
ǡ����![]() �ϵĵ�
�ϵĵ�![]() �غϣ�չ�����ۺ�
�غϣ�չ�����ۺ�![]() �ֱ�
�ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ������
������![]() �������н��ۣ���
�������н��ۣ���![]() ����
����![]() ����
����![]() �����ı���
�����ı���![]() �����Σ���
�����Σ���![]() ��������ȷ���۵������______.
��������ȷ���۵������______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��M��ƽ���ı���ABCD��AB�ߵ��е㣬CM��BD�ཻ�ڵ�E����ƽ���ı���ABCD�����Ϊ1����ͼ����Ӱ���ֵ������__________.
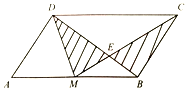
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʦ�������˱�ѧ��ѧ�����������������������Ƴ�����ͼ��ͼ1���Ͳ�����������ͼ��ͼ2������������ͼ��ī���ڸ���һ����.
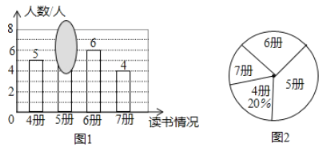
��1��������ͼ�б��ڸǵ����������������ƽ��������λ����
��2������ֲ��������⼸�ˣ���֪���ٵĶ���6�ᣬ������֮ǰ�����ݺϲ����ֲ�������λ��û�ı䣬����ಹ����__________��.�Ӳ���������ѧ���Ķ��������ƽ������֮ǰ���______________.�����С�����䣩.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O�����ߣ��е�ΪB��OA����O�ڵ�C������C�����߽�AB�ڵ�D������BAO��30����CD��2��
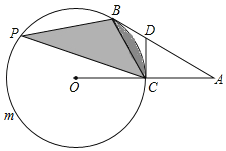
��1�����O�İ뾶��
��2������P��![]() ���˶������P��ֱ��BC�ľ���Ϊx��ͼ����Ӱ���ֵ����Ϊy����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
���˶������P��ֱ��BC�ľ���Ϊx��ͼ����Ӱ���ֵ����Ϊy����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������۹�˾���ֱ������������ͺŻ�����һ���£�������ѡ��һ�ֳ������ۣ���ÿ��������Ϊx�������ۼ��ͻ�����ÿ�����۵�����Ϊy1(��Ԫ)����֪ÿ�����ͻ���������Ϊ(m+6)��Ԫ��(m�dz�����9��m��11)��ÿ�»���֧����������8��Ԫ������������ÿ����������ۼ��ͻ���25�������������ͻ�����ÿ�µ�����y2(��Ԫ)��x�ĺ�����ϵʽΪy2=ax2+bx-25���ҵ�x��10ʱ��y2��20����x��20ʱ��y2��55������������ÿ��������������ͻ���40����
(1)�ֱ����y1��y2��x�ĺ�����ϵʽ����ȷ��x��ȡֵ����Χ��
(2)�ֱ�������������ֻ��������������(�����������ֵ����ֵ��������ֵ����ʽ�ӱ�ʾ)
(3)Ϊ�����������ù�˾Ӧ��ѡ���������ֻ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
��![]() ��
��![]() ����
����![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ��
��![]() ���ۺ�
���ۺ�![]() ����
����![]() ��.��
��.��![]() ǡΪ���������Σ���
ǡΪ���������Σ���![]() �ij�Ϊ______.
�ij�Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
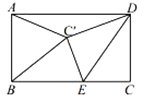
����Ŀ��ij��ѧ�С����һ�λ�У���һ����ѧ����������̽����
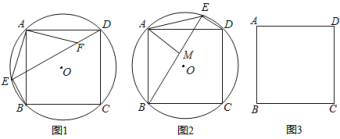
�����ⷢ�֣���ͼ1��������ABCD���ĸ����㶼�ڡ�O�ϣ�����E�ڻ�AB�ϣ�F��DE�ϵ�һ�㣬��DF��BE����˵������ADF�ա�ABE��
����ʽ̽������ͼ2������E�ڻ�AD�ϣ�����A��AM��BE����˵���߶�BE��DE��AM֮�����������ϵ��BE��DE��2AM��
��������⣩��ͼ3����������ABCD�У�CD��2![]() ������P����PD��2���ҡ�BPD��90������ֱ��д����A��BP�ľ��룮
������P����PD��2���ҡ�BPD��90������ֱ��д����A��BP�ľ��룮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com