
【题目】如图,点A是抛物线![]() 对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为______________.
对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为______________.

【答案】(2,2)或(2,-1)
【解析】
∵抛物线y=x2-4x对称轴为直线x=-![]()
∴设点A坐标为(2,m),
如图所示,作AP⊥y轴于点P,作O′Q⊥直线x=2,
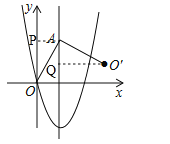
∴∠APO=∠AQO′=90°,
∴∠QAO′+∠AO′Q=90°,
∵∠QAO′+∠OAQ=90°,
∴∠AO′Q=∠OAQ,
又∠OAQ=∠AOP,
∴∠AO′Q=∠AOP,
在△AOP和△AO′Q中,
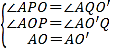
∴△AOP≌△AO′Q(AAS),
∴AP=AQ=2,PO=QO′=m,
则点O′坐标为(2+m,m-2),
代入y=x2-4x得:m-2=(2+m)2-4(2+m),
解得:m=-1或m=2,
∴点A坐标为(2,-1)或(2,2),
故答案是:(2,-1)或(2,2).


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为![]() 元的苹果,物价部门规定每箱售价不得高于
元的苹果,物价部门规定每箱售价不得高于![]() 元,市场调查发现,若每箱以
元,市场调查发现,若每箱以![]() 元的价格销售,平均每天销售
元的价格销售,平均每天销售![]() 箱,价格每提高
箱,价格每提高![]() 元,平均每天少销售
元,平均每天少销售![]() 箱.
箱.
求该批发商平均每天的销售利润![]() (元)与销售价
(元)与销售价![]() (元/箱)之间的函数关系式.当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
(元/箱)之间的函数关系式.当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,AC与⊙O交于D,OE∥BD交⊙O于E.
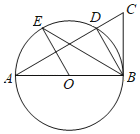
(1)求证:BE平分∠ABD.
(2)当∠A=∠E,BC=2时,求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+2x+3与x轴交于点A,B(点A在点B的左边),与y轴交于点C.
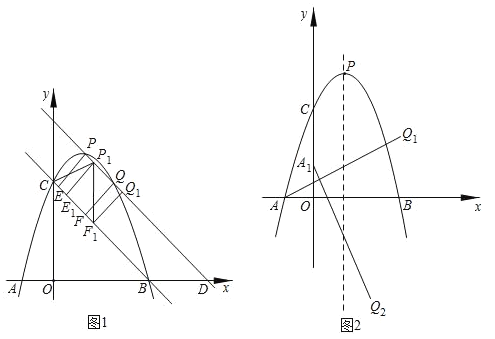
(1)如图1,点P,Q都在直线BC上方的抛物线上,且点P的横坐标比点Q的横坐标小1,直线PQ与x轴交于点D,过点P,Q作直线BC的垂线,垂足分别为点E,F.当PE+QF的值最大时,将四边形PEFQ沿射线PQ方向平移,记平移过程中的四边形PEFQ为P1E1F1Q1,连接CP1,P1F1,求CP1+P1F1+![]() Q1D的最小值,并求出对应的点Q1的坐标.
Q1D的最小值,并求出对应的点Q1的坐标.
(2)如图2,对于满足(1)中条件的点Q1,将线段AQ1绕原点O顺时针旋转90°,得线段A1Q2,点M是抛物线对称轴上一点,点N是坐标平面内一点,点N1是点N关于直线A1Q2的对称点,若以点A1,Q1,M,N1为顶点的四边形是一个矩形,请直接写出所有符合条件的点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中的弦BC等于⊙O的半径,延长BC到D,使BC=CD,点A为优弧BC上的一个动点,连接AD,AB,AC,过点D作DE⊥AB,交直线AB于点E,当点A在优弧BC上从点C运动到点B时,则DE+AC的值的变化情况是( )
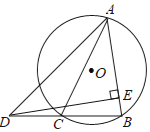
A.不变B.先变大再变小C.先变小再变大D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长城汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润45万元,那么该月需售出多少辆汽车?(注:销售利润=销售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
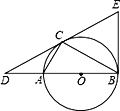
【题目】已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA∶AB=1∶2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技公司推出一款新的电子产品,该产品有三种型号.通过市场调研后,按三种型号受消费者喜爱的程度分别对A型、B型、C型产品在成本的基础上分别加价20%,30%,45%出售(三种型号的成本相同).经过一个季度的经营后,发现C型产品的销量占总销量的![]() ,且三种型号的总利润率为35%.第二个季度,公司决定对A型产品进行升级,升级后A产品的成本提高了25%,销量提高了20%;B、C产品的销量和成本均不变,且三种产品在二季度成本基础上分别加价20%,30%,45%出售,则第二个季度的总利润率为______.
,且三种型号的总利润率为35%.第二个季度,公司决定对A型产品进行升级,升级后A产品的成本提高了25%,销量提高了20%;B、C产品的销量和成本均不变,且三种产品在二季度成本基础上分别加价20%,30%,45%出售,则第二个季度的总利润率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂生产一种半成品食材,成本为2元/千克,每天的产量![]() (百千克)与销售价格
(百千克)与销售价格![]() (元/千克)满足函数关系式
(元/千克)满足函数关系式![]() ,从市场反馈的信息发现,该半成品食材每天的市场需求量
,从市场反馈的信息发现,该半成品食材每天的市场需求量![]() (百千克)与销售价格
(百千克)与销售价格![]() (元/千克)满足一次函数关系,部分数据如表:
(元/千克)满足一次函数关系,部分数据如表:
销售价格 | 2 | 4 | …… | 10 |
市场需求量 | 12 | 10 | …… | 4 |
已知按物价部门规定销售价格![]() 不低于2元/千克且不高于10元/千克.
不低于2元/千克且不高于10元/千克.
(1)直接写出![]() 与
与![]() 的函数关系式,并注明自变量
的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(2)当每天的产量小于或等于市场需求量时,这种半成品食材能全部售出,而当每天的产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃.
①当每天的半成品食材能全部售出时,求![]() 的取值范围;
的取值范围;
②求厂家每天获得的利润y(百元)与销售价格![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,当![]() 为______元/千克时,利润
为______元/千克时,利润![]() 有最大值;若要使每天的利润不低于24(百元),并尽可能地减少半成品食材的浪费,则
有最大值;若要使每天的利润不低于24(百元),并尽可能地减少半成品食材的浪费,则![]() 应定为______元/千克.
应定为______元/千克.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com