
【题目】抛物线y=﹣x2+2x+3与x轴交于点A,B(点A在点B的左边),与y轴交于点C.
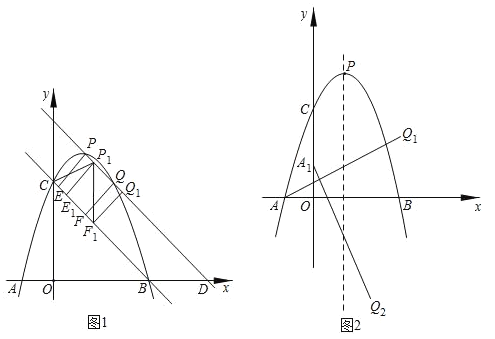
(1)如图1,点P,Q都在直线BC上方的抛物线上,且点P的横坐标比点Q的横坐标小1,直线PQ与x轴交于点D,过点P,Q作直线BC的垂线,垂足分别为点E,F.当PE+QF的值最大时,将四边形PEFQ沿射线PQ方向平移,记平移过程中的四边形PEFQ为P1E1F1Q1,连接CP1,P1F1,求CP1+P1F1+![]() Q1D的最小值,并求出对应的点Q1的坐标.
Q1D的最小值,并求出对应的点Q1的坐标.
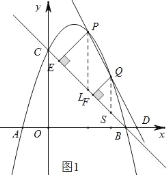
(2)如图2,对于满足(1)中条件的点Q1,将线段AQ1绕原点O顺时针旋转90°,得线段A1Q2,点M是抛物线对称轴上一点,点N是坐标平面内一点,点N1是点N关于直线A1Q2的对称点,若以点A1,Q1,M,N1为顶点的四边形是一个矩形,请直接写出所有符合条件的点N的坐标.
【答案】(1)CP1+P1F1+![]() Q1D的最小值=6,Q1(3,2);(2)N的坐标为(
Q1D的最小值=6,Q1(3,2);(2)N的坐标为(![]() )或(
)或(![]() ),(
),(![]() )或(
)或(![]() ).
).
【解析】
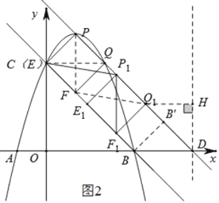
(1)如图1,过P作PL∥y轴交直线BC于L,过Q作QS∥y轴交BC于S,由抛物线解析式可求与xy轴交点,即可求出BC点坐标,进而求出直线BC解析式,设P(t,﹣t2+2t+3),则L(t,﹣t+3),Q(t+1,﹣t2+4),S(t+1,﹣t+2),将PE+QF转化为![]() (PL+QS),得到关于t的二次函数解析式即可求出当t=1时,PE+QF最小,此时P(1,4),Q(2,3),E点与C点重合,F点坐标为(1,2),PQ与BC平行.四边形PEFQ是正方形,进而得出P1F1=PF=2,CP1=FQ1,作D(5,0)作DH⊥x轴,过Q1作Q1H⊥DH,可得Q1H=
(PL+QS),得到关于t的二次函数解析式即可求出当t=1时,PE+QF最小,此时P(1,4),Q(2,3),E点与C点重合,F点坐标为(1,2),PQ与BC平行.四边形PEFQ是正方形,进而得出P1F1=PF=2,CP1=FQ1,作D(5,0)作DH⊥x轴,过Q1作Q1H⊥DH,可得Q1H=![]() Q1D,故当点F、Q1、H三点在同一直线上,FQ1H⊥DH轴时,FQ1+Q1H最小,即CP1+P1F1+
Q1D,故当点F、Q1、H三点在同一直线上,FQ1H⊥DH轴时,FQ1+Q1H最小,即CP1+P1F1+![]() Q1D的值最小,由点F坐标(1,2)可得Q1(3,2),H(5,2),FH=4.即可解题.
Q1D的值最小,由点F坐标(1,2)可得Q1(3,2),H(5,2),FH=4.即可解题.
(2)根据旋转90°点坐标变化规律可知A1(0,1),Q2(2,﹣3).根据抛物线解析式可得抛物线对称轴为x=1,设M为(1,m),可得A1M2=m2﹣2m+2,A1Q22=10,MQ22=m2﹣4m+8,分三种情况求出M,进而根据平移求出N1,再根据直线对称求出对称点连线与对称轴交点,即对称点连线的中点求出点N坐标即可.
解:(1)如图1,过P作PL∥y轴交直线BC于L,过Q作QS∥y轴交BC于S,
抛物线y=﹣x2+2x+3与x轴交于点A,B(点A在点B的左边),与y轴交于点C.
∴A(﹣1,0),B(3,0),C(0,3);
∴直线BC的解析式为y=﹣x+3,
设P(t,﹣t2+2t+3),则L(t,﹣t+3),Q(t+1,﹣t2+4),S(t+1,﹣t+2),
PL=﹣t2+2t+3﹣(﹣t+3)=﹣t2+3t,QS=﹣t2+4﹣(﹣t+2)=﹣t2+t+2,
∵PE⊥BC,QF⊥BC,PL∥y轴,QS∥y轴
∴∠PEL=∠QFS=∠BOC=90°,∠PLE=∠QSF=∠BCO=45°
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() (﹣t2+t+2)=
(﹣t2+t+2)=![]()
∵![]() ,0<t<3,
,0<t<3,
∴当t=1时,PE+QF有最大值为![]() ,此时P(1,4),Q(2,3),
,此时P(1,4),Q(2,3),
∴直线PQ解析式为y=﹣x+5,PQ=![]() .H(0,5),D(5,0)
.H(0,5),D(5,0)
∴BD=2
如图2,过B作BB′⊥PQ于B′,在Rt△BB′D中,BB′=BDsin∠BDB′=2sin45°=![]() ,
,
∴PE=QF=P1E1=Q1F1=BB′=![]() (平行线间距离相等)
(平行线间距离相等)
∴PQ=QF
∵QF⊥BC,BC∥PQ,
∴QF⊥PQ,
∴四边形PEFQ是正方形,
∵∠QEP=∠EPQ=45°,
∴E点与C点重合,F点坐标为(1,2)
由平移知P1E1F1Q1与正方形PEFQ是全等形,
∴P1F1=PF=2.易证Rt△CPP1≌Rt△FQQ1,
∴CP1=FQ1
作D(5,0)作DH⊥x轴,过Q1作Q1H⊥DH,
∵∠HDQ1=45°,
∴Q1H=![]() Q1D,
Q1D,
当点F、Q1、H三点在同一直线上,FQ1H⊥DH轴时,FQ1+Q1H最小,即CP1+P1F1+![]() Q1D的值最小,
Q1D的值最小,
∵此时,F点坐标为(1,2),Q1(3,2),(5,2),FH=4.
∴CP1+P1F1+![]() Q1D的最小值=4+2=6,Q1(3,2).
Q1D的最小值=4+2=6,Q1(3,2).
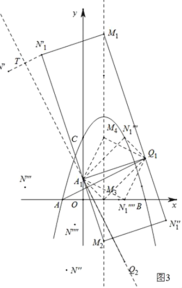
(2)如图3,将线段AQ1绕原点O顺时针旋转90°得线段A1Q2,根据旋转90°点坐标变化规律可知A1(0,1),Q2(2,﹣3).
∵抛物线对称轴为x=![]() =1,设M(1,m),∴A1M2=(1﹣0)2+(m﹣1)2=m2﹣2m+2
=1,设M(1,m),∴A1M2=(1﹣0)2+(m﹣1)2=m2﹣2m+2
A1Q22=(0﹣3)2+(1﹣2)2=10
MQ22=(1﹣3)2+(m﹣2)2=m2﹣4m+8
若A1M为斜边,则由题意得:![]() ,
,
10+m2﹣4m+8=m2﹣2m+2
解得:m=8,
M1(1,8)
若Q2M为斜边则由题意得:![]() ,
,
m2﹣2m+2+10=m2﹣4m+8
m=﹣2,
∴M2(1,﹣2)
若A1Q2为斜边,则由题意得:![]() ,
,
即:(m2﹣2m+2)+(m2﹣4m+8)=10.
解得m=0或m=3,
即∴M3(1,0)或M4(1,3).
∵四边形A1MQ1N1是矩形,
∴根据点的平移可知N1坐标为(﹣2,7)或(4,﹣1)或(1,0)或(1,3),
∵N'1与N'关于直线A1Q2对称,
∴N'1N'⊥A1Q2,T为N'1N'中点,
由点坐标可求直线A1Q2解析式为:y=﹣2x+1,
直线N'1N'解析式为:y=![]() +8,
+8,
故T坐标为(![]() ,
,![]() ),
),
∴N'坐标为(![]() )
)
同理可得N“为(![]() ),(
),(![]() )或(
)或(![]() )
)
综上所述:N的坐标为(![]() )或(
)或(![]() ),(
),(![]() )或(
)或(![]() ).
).


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF∥BC,AF与CE的延长线相交于点F,连接BF.

(1)求证:四边形AFBD是平行四边形;
(2)将下列命题填写完整,并使命题成立(图中不再添加其它的点和线):
①当△ABC满足条件AB=AC时,四边形AFBD是 形;
② 当△ABC满足条件 时,四边形AFBD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D在AB的延长线上,点C、E是⊙O上的两点,CE=CB,![]() ,延长AE交BC的延长线于点F.
,延长AE交BC的延长线于点F.

(1)求证:CD是⊙O的切线;
(2)求证:CE=CF
(3)若BD=1,![]() ,求直径AB的长.
,求直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米. 点
厘米. 点![]() 沿
沿![]() 边从
边从![]() 开始向点
开始向点![]() 以2厘米/秒的速度移动;点
以2厘米/秒的速度移动;点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以1厘米/秒速度移动.如果
以1厘米/秒速度移动.如果![]() 、
、![]() 同时出发,用
同时出发,用![]() (秒)表示移动的时间
(秒)表示移动的时间![]() ,那么:
,那么:
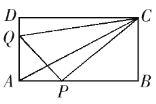
(1)当![]() 为何值时,
为何值时,![]() 为等腰直角三角形?
为等腰直角三角形?
(2)求四边形![]() 的面积;提出一个与计算结果有关的结论;
的面积;提出一个与计算结果有关的结论;
(3)当![]() 为何值时,以点
为何值时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的QO分别与BC、AC交于点D、E,过点D作DF⊥AC于点F.
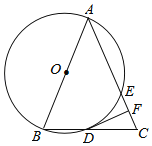
(1)求证:DF是⊙O的切线;
(2)求证:∠EDF=∠DAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是抛物线![]() 对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为______________.
对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘油轮在海中航行,在A点看到小岛B在A的北偏东25°方向距离60海里处,油轮沿北偏东70°方向航行到C处,看到小岛B在C的北偏西50°方向,则油轮从A航行到C处的距离是( )海里.(结果保留整数)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.74,
≈1.74,![]() ≈2.45)
≈2.45)
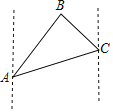
A.66.8B.67C.115.8D.116
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是平行四边形ABCD的AB边的中点,CM与BD相交于点E,设平行四边形ABCD的面积为1,则图中阴影部分的面积是__________.
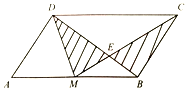
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com