
ЁОЬтФПЁПЮЊгНгЁАСљвЛЁБЖљЭЏНкЃЌФГЖљЭЏЦЗХЦЭцОпзЈТєЕъЙКНјСЫAЁЂBСНжжЭцОпЃЌЦфжаAРрЭцОпЕФНјМлБШBЭцОпЕФНјМлУПИіЖр3дЊЃЌОЕїВщЃКгУ900дЊЙКНјAРрЭцОпЕФЪ§СПгыгУ750дЊЙКНјBРрЭцОпЕФЪ§СПЯрЭЌ
ЃЈ1ЃЉЧѓAЁЂBСНРрЭцОпЕФНјМлЗжБ№ЪЧУПИіЖрЩйдЊЃП
ЃЈ2ЃЉИУЭцОпЕъЙВЙКНјСЫAЁЂBСНРрЭцОпЙВ100ИіЃЌШєЭцОпЕъНЋУПИіAРрЭцОпЖЈМлЮЊ30дЊГіЪлЃЌУПИіBРрЭцОпЖЈМл25дЊГіЪлЃЌЧвШЋВПЪлГіКѓЫљЛёЕУРћШѓВЛЩйгк1080дЊЃЌдђЩЬЕъжСЩйЙКНјAРрЭцОпЖрЩйИіЃП
ЁОД№АИЁПЃЈ1ЃЉAЕФНјМлЪЧ18дЊЃЌBЕФНјМлЪЧ15дЊЃЛЃЈ2ЃЉжСЩйЙКНјAРрЭцОп40ИіЃЎ
ЁОНтЮіЁП
(1)ЩшBЕФНјМлЮЊxдЊЃЌдђAЕФНјМлЪЧЃЈx+3ЃЉдЊЃЛИљОнгУ900дЊЙКНјAРрЭцОпЕФЪ§СПгыгУ750дЊЙКНјBРрЭцОпЕФЪ§СПЯрЭЌетИіЕШСПЙиЯЕСаГіЗНГЬМДПЩЃЎ
(2)ЩшAЭцОпaИіЃЌдђBЭцОп(100a)ИіЃЌНсКЯЁАЭцОпЕъНЋУПИіAРрЭцОпЖЈМлЮЊ30дЊГіЪлЃЌУПИіBРрЭцОпЖЈМл25дЊГіЪлЃЌЧвШЋВПЪлГіКѓЫљЛёЕУРћШѓВЛЩйгк1080дЊЁБСаГіВЛЕШЪНВЂНтД№ЃЎ
НтЃКЃЈ1ЃЉЩшBЕФНјМлЮЊxдЊЃЌдђAЕФНјМлЪЧЃЈx+3ЃЉдЊЃЌ
гЩЬтвтЕУ![]() ЃЌ
ЃЌ
НтЕУЃКx=15ЃЌ
ОМьбщx=15ЪЧдЗНГЬЕФНтЃЎ
Ыљвд15+3=18ЃЈдЊЃЉ
Д№ЃКAЕФНјМлЪЧ18дЊЃЌBЕФНјМлЪЧ15дЊЃЛ
ЃЈ2ЃЉЩшAЭцОпaИіЃЌдђBЭцОпЃЈ100ЉaЃЉИіЃЌ
гЩЬтвтЕУЃК12a+10ЃЈ100ЉaЃЉЁн1080ЃЌ
НтЕУЃКaЁн40ЃЎ
Д№ЃКжСЩйЙКНјAРрЭцОп40ИіЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
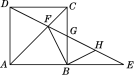
ЁОЬтФПЁПШчЭМЃЌEЮЊе§ЗНаЮABCDЕФБпABЕФбгГЄЯпЩЯвЛЕуЃЌDEНЛACгкЕуFЃЌНЛBCгкЕуGЃЌHЮЊGEЕФжаЕуЃЎ
ЧѓжЄЃКFBЁЭBH.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
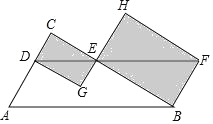
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌBC=4ЃЌBA=5ЃЌЕуDдкБпACЩЯЕФвЛЖЏЕуЃЌЙ§ЕуDзїDEЁЮABНЛБпBCгкЕуEЃЌЙ§ЕуBзїBFЁЭBCНЛDEЕФбгГЄЯпгкЕуFЃЌЗжБ№вдDEЃЌEFЮЊЖдНЧЯпЛОиаЮCDGEКЭОиаЮHEBFЃЌдђдкDДгAЕНCЕФдЫЖЏЙ§ГЬжаЃЌЕБОиаЮCDGEКЭОиаЮHEBFЕФУцЛ§КЭзюаЁЪБЃЌдђEFЕФГЄЖШЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкАыОЖЮЊ4ЕФ![]() жаЃЌ
жаЃЌ![]() ЮЊжБОЖЃЌЯв
ЮЊжБОЖЃЌЯв![]() ЧвЙ§АыОЖ
ЧвЙ§АыОЖ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЮЊ
ЮЊ![]() ЩЯвЛЖЏЕуЃЌ
ЩЯвЛЖЏЕуЃЌ![]() гкЕу
гкЕу![]() ЃЌМДЕу
ЃЌМДЕу![]() дквд
дквд![]() ЮЊжБОЖЕФдВЩЯЃЌЕБ
ЮЊжБОЖЕФдВЩЯЃЌЕБ![]() ДгЕу
ДгЕу![]() ГіЗЂЫГЪБеыдЫЖЏЕНЕу
ГіЗЂЫГЪБеыдЫЖЏЕНЕу![]() ЪБЃЌЕу
ЪБЃЌЕу![]() ЫљОЙ§ЕФТЗОЖГЄЮЊЃЈ ЃЉ
ЫљОЙ§ЕФТЗОЖГЄЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
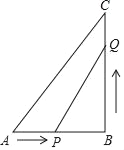
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЁїABCжаЃЌЁЯB=90ЁуЃЌAB=5cmЃЌBC=7cmЃЎЕуPДгЕуAПЊЪМбиABБпЯђЕуBвд1cm/sЕФЫйЖШвЦЖЏЃЌЕуQДгЕуBПЊЪМбиBCБпЯђЕуCвд2cm/sЕФЫйЖШвЦЖЏЃЎ
ЃЈ1ЃЉШчЙћPЃЌQЗжБ№ДгAЃЌBЭЌЪБГіЗЂЃЌФЧУДМИУыКѓЃЌЁїPBQЕФУцЛ§ЕШгк6cm2ЃП
ЃЈ2ЃЉдкЃЈ1ЃЉжаЃЌЁїPQBЕФУцЛ§ФмЗёЕШгк8cm2ЃПЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНГЕЭЌЪБДгAЕиГіЗЂЃЌвдИїздЕФЫйЖШдШЫйЯђBЕиааЪЛЃЌМзГЕЯШЕНBЕиЃЌЭЃГЕ1аЁЪБАДдЫйЖШдШЫйЗЕЛиЃЌжБЕНСНГЕЯргіЃЎввГЕЫйЖШЪЧ60ЧЇУз/ЪБЃЌШчЭМЪЧСНГЕжЎМфЕФОрРыyЃЈИЩУзЃЉгыввГЕааЪЛЪБМфxЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЭМЯѓЃЌдђЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
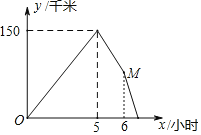
A.AЁЂBСНЕиЯрОр150ЧЇУз
B.МзГЕЫйЖШЪЧ100ЧЇУз/ЪБ
C.ввГЕДгГіЗЂЕНгыМзГЕЯргіЙВгУ![]() аЁЪБ
аЁЪБ
D.ЕуMЕФзнзјБъЮЊ90
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
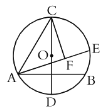
ЁОЬтФПЁПвбжЊЃКХзЮяЯпyЃНax2Љ3ax+4гыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌЧвABЃН5ЃЎ
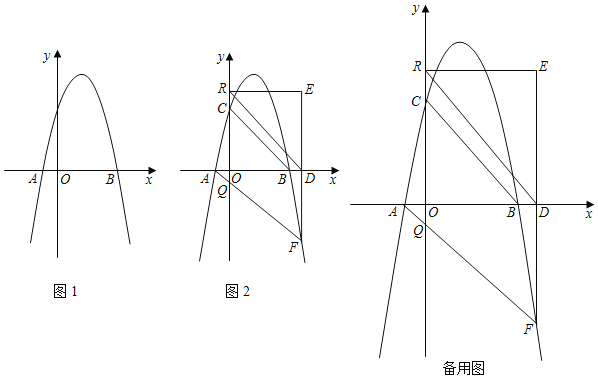
ЃЈ1ЃЉШчЭМ1ЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌХзЮяЯпгыyжсНЛгкЕуCЃЌFЪЧЕкЫФЯѓЯоХзЮяЯпЩЯвЛЕуЃЌFDЁЭxжсЃЌДЙзуЮЊDЃЌEЪЧFDбгГЄЯпЩЯвЛЕуЃЌERЁЭyжсЃЌДЙзуЮЊRЃЌFAНЛyжсгкЕуQЃЌШєBCЁЮRDЃЎЧѓжЄЃКOQЃНCRЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌдкRDЩЯШЁвЛЕуMЃЌбгГЄOMНЛЯпЖЮDEгкЕуNЃЌREНЛХзЮяЯпгкЕуTЃЈЕуTдкХзЮяЯпЖдГЦжсЕФгвВрЃЉЃЌСЌНгMTЁЂNTЃЌЧвTMЁЭOMЃЌ![]() ЃН
ЃН![]() ЃЌHЪЧAFЩЯвЛЕуЃЌЕБЁЯDHFЃН135ЁуЪБЃЌЧѓЕуHЕФзјБъЃЎ
ЃЌHЪЧAFЩЯвЛЕуЃЌЕБЁЯDHFЃН135ЁуЪБЃЌЧѓЕуHЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдк 10ЁС6 ЕФе§ЗНаЮЭјИёжаЃЌУПИіаЁе§ЗНаЮЕФБпГЄОљЮЊ 1ЃЌЯпЖЮ AB ЕФЖЫЕу AЁЂB ОљдкаЁе§ЗНаЮЕФЖЅЕуЩЯЃЎ
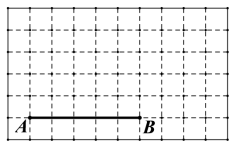
ЃЈ1ЃЉдкЭМжаЛГівд AB ЮЊвЛбќЕФЕШбќЁїABCЃЌЕу C дкаЁе§ЗНаЮЖЅЕуЩЯЃЌЁїABC ЮЊЖлНЧШ§НЧаЮЃЌЧвЁїABC ЕФУцЛ§ЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкЭМжаЛГівд AB ЮЊаББпЕФжБНЧШ§НЧаЮ ABDЃЌ Еу DдкаЁе§ЗНаЮЕФЖЅЕуЩЯЃЌЧв AD>BDЃЛ
ЃЈ3ЃЉСЌНг CDЃЌЧыФужБНгаДГіЯпЖЮ CD ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛСОПьГЕДгМзЕиЪЛЭљввЕиЃЌвЛСОТ§ГЕДгввЕиЪЛЭљМзЕиЃЌСНГЕЭЌЪБГіЗЂЃЌдШЫйааЪЛЃЎЩшааЪЛЕФЪБМфЮЊxЃЈЪБЃЉЃЌСНГЕжЎМфЕФОрРыЮЊyЃЈЧЇУзЃЉЃЌШчЭМжаЕФелЯпБэЪОДгСНГЕГіЗЂжСПьГЕЕНДяввЕиЙ§ГЬжаyгыxжЎМфЕФКЏЪ§ЙиЯЕЃЎвбжЊСНГЕЯргіЪБПьГЕБШТ§ГЕЖрааЪЛ40ЧЇУзЃЌШєПьГЕДгМзЕиЕНДяввЕиЫљашЪБМфЮЊtЪБЃЌдђtЕФжЕЮЊ_____ЃЎ
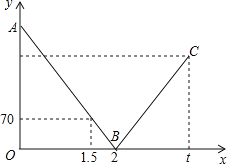
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com