
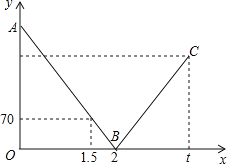
【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),如图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,则t的值为_____.
科目:初中数学 来源: 题型:
【题目】为迎接“六一”儿童节,某儿童品牌玩具专卖店购进了A、B两种玩具,其中A类玩具的进价比B玩具的进价每个多3元,经调查:用900元购进A类玩具的数量与用750元购进B类玩具的数量相同
(1)求A、B两类玩具的进价分别是每个多少元?
(2)该玩具店共购进了A、B两类玩具共100个,若玩具店将每个A类玩具定价为30元出售,每个B类玩具定价25元出售,且全部售出后所获得利润不少于1080元,则商店至少购进A类玩具多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随点
的位置随点![]() 的位置变化而变化.
的位置变化而变化.
(1)如图1,当点![]() 在菱形
在菱形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
(2)当点![]() 在菱形
在菱形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3) 如图4,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2mx+m2﹣3(m是常数)
(1)证明:无论m取什么实数,该抛物线与x轴都有两个交点.
(2)设抛物线的顶点为A,与x轴的两个交点分别为B、D,点B在点D的右侧,与y轴的交点为 C.
①若点P为△ABD的外心,求点P的坐标(用含m的式子表示);
②当|m|≤![]() ,m≠0时,△ABC的面积是否有最大值?如果有,请求出最大值;如果没有,请说明理由.
,m≠0时,△ABC的面积是否有最大值?如果有,请求出最大值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销A、B两种商品,现有如下信息:
信息1:A、B两种商品的进货单价之和是3元;
信息2:A商品零售单价比进货单价多1元,B商品零售单价比进货单价的2倍少1元;
信息3:按零售单价购买A商品3件和B商品2件,共付12元.
请根据以上信息,解答下列问题:
(1)求A、B两种商品的零售单价;
(2)该商店平均每天卖出A商品500件和B商品1500件.经调查发现,A种商品零售单价每降0.1元,A种商品每天可多销售100件.商店决定把A商品的零售单价下降m(m>0)元,B商品的零售单价和销量都不变,在不考虑其他因素的条件下,当m为多少时,商品每天销售A、B两种商品获取的总利润为2000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张如图所示的长为![]() ,宽为
,宽为![]() 的小长方形纸片,按如图的方式不重叠地放在矩形
的小长方形纸片,按如图的方式不重叠地放在矩形![]() 中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为
中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为![]() ,当
,当![]() 的长度变化时,按照同样的放置方式,
的长度变化时,按照同样的放置方式,![]() 始终保持不变,则
始终保持不变,则![]() ,
,![]() 满足的关系式为( )
满足的关系式为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华星商店准备从阳光机械厂购进甲、乙两种零件进行销售,若一个甲种零件的进价比一个乙种零件的进价多50元,用4000元购进甲种零件的数量是用1500元购进乙种零件的数量的2倍.
(1)求每个甲种零件,每个乙种零件的进价分别为多少元?
(2)华星商店甲种零件每件售价为260元,乙种零件每件售价为190元,商店根据市场需求.决定向该厂购进一批零件、且购进乙种零件的数量比购进甲种零件的数量的2倍还多4个,若本次购进的两种零件全部售出后,总获利不少于2400元、求该商店本次购进甲种零件至少是多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c与x轴交于A(-1,0)、B两点,与y轴交于点C,OC = 3OA,D为抛物线的顶点.
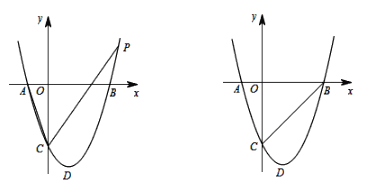
(1)求抛物线的解析式;
(2)若点P在抛物线上,tan∠ACP = ![]() ,求P点的坐标;
,求P点的坐标;
(3)将抛物线沿直线y = x + b翻折,若点D的对应点E落在△ABC的内部(含△ABC的边)时,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com