
【题目】已知抛物线y=x2+bx+c与x轴交于A(-1,0)、B两点,与y轴交于点C,OC = 3OA,D为抛物线的顶点.
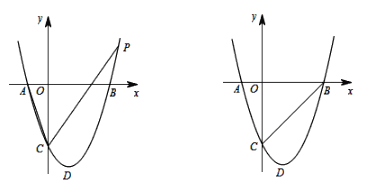
(1)求抛物线的解析式;
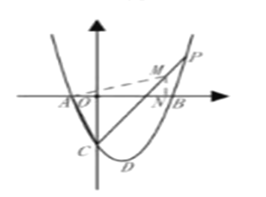
(2)若点P在抛物线上,tan∠ACP = ![]() ,求P点的坐标;
,求P点的坐标;
(3)将抛物线沿直线y = x + b翻折,若点D的对应点E落在△ABC的内部(含△ABC的边)时,求b的取值范围.
【答案】(1) y=x2-2x-3;(2) P(![]() ,
,![]() );(3)
);(3) ![]() ≤b≤-2.
≤b≤-2.
【解析】
(1)由A(-1,0)和OC = 3OA确定C点坐标,然后使用待定系数法解答即可;
(2)过A作AM⊥AC交CP于M ,tan∠ACP =![]() ,则△AOC∽△MNA,有
,则△AOC∽△MNA,有![]() ,则,MN=
,则,MN=![]() AO=
AO=![]() ,AN=
,AN=![]() OC=4,可得ON=AN-AO=3,则M(3,
OC=4,可得ON=AN-AO=3,则M(3,![]() ),再确定CM的解析式,在于抛物线解析式联立即可完成解答;
),再确定CM的解析式,在于抛物线解析式联立即可完成解答;
(3)分E在A上和E在AO与BC的交点两种情况讨论求出临界点即可.
解:∵A(-1,0),OC = 3OA
∴C(0,-3)
则有![]() 即
即![]()
∴抛物线的解析式为y=x2-2x-3;
(2)过A作AM⊥AC交CP于M,过M作MN⊥x轴,垂足为N
∴tan∠ACP=![]()
易证∠ACO=∠MAN, ∠AOC=∠MNA,
![]() ∴△AOC∽△MNA
∴△AOC∽△MNA
∴![]()
∴MN=![]() AO=
AO=![]() ,AN=
,AN=![]() OC=4
OC=4
∴ON=AN-AO=3
∴M(3,![]() )
)
利用待定系数法可得CM的解析式为:y=![]()
联立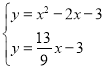 解得
解得![]() 或
或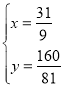
∴P(![]() ,
,![]() )
)
(3)tan∠ADH=![]()
∴![]()
①E在A上时,DE的中点(0,-3)在y=-![]() x+b上,解得b=-2
x+b上,解得b=-2
②E在AO与BC的交点,BC的解析式为y=x-3;AO的解析式为y=-2x-2
联立可得E(![]() ,-
,-![]() )
)
∴DE的中点为(![]() ,-
,-![]() )在y=-
)在y=-![]() x+b上,解得b=-
x+b上,解得b=-![]()
∴![]() ≤b≤-2
≤b≤-2


科目:初中数学 来源: 题型:
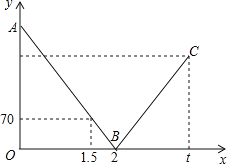
【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为x(时),两车之间的距离为y(千米),如图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系.已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,则t的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
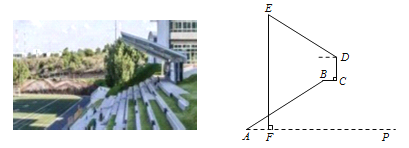
【题目】如图是某户外看台的截面图,长10m的看台AB与水平地面AP的夹角为35°,与AP平行的平台BC长为1.9m,点F是遮阳棚DE上端E正下方在地面上的一点,测得AF=2m,在挡风墙CD的点D处测得点E的仰角为26°,求遮阳棚DE的长. (参考数据:sin35°≈0.57,cos35°≈0.82, sin26°≈0.44,cos26°≈0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
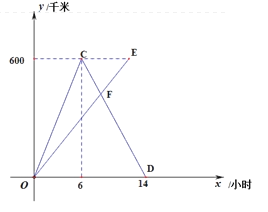
【题目】甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)AB两城之间的距离为_______km.
(2)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(3)乙用8小时到达B城,求乙车速度及他们相遇的时间.
(4)直接写出两车何时相距80km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年,《中国诗词大会》、《朗读者》,《经典咏流传》、《国家宝藏》等文化类节目相继走红,被人们称为“清流综艺”,六中上智中学某兴趣小组想了解全校学生对这四个节目的喜爱情况,随机抽取了部分学生进行调查统计,要求每名学生选出一个自己最喜爱的节目,并将调查结果给制成如下统计图(其中《中国诗词大会》,《朗读者》,《经典咏流传》,《国家宝藏》分别用A,B,C.D表示),请你结合图中信息解答下列问题:
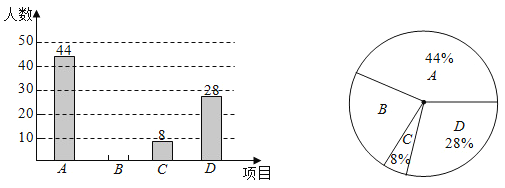
(1)本次调查的学生人数是 人:
(2)请把条形统计图补充完整.
(3)在扇形统计图中,B对应的圆心角的度数是 .
(4)已知六中上智中学共有3200名学生,请根据样本估计全校最喜爱《朗读者》的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
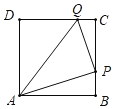
【题目】已知,如图,正方形![]() 的边长为4厘米,点
的边长为4厘米,点![]() 从点
从点![]() 出发,经
出发,经![]() 沿正方形的边以2厘米/秒的速度运动;同时,点
沿正方形的边以2厘米/秒的速度运动;同时,点![]() 从点
从点![]() 出发以1厘米/秒的速度沿
出发以1厘米/秒的速度沿![]() 向点
向点![]() 运动,设运动时间为t秒,
运动,设运动时间为t秒,![]() 的面积为
的面积为![]() 平方厘米.
平方厘米.
(1)当![]() 时,
时,![]() 的面积为__________平方厘米;
的面积为__________平方厘米;
(2)求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(3)当点![]() 在线段
在线段![]() 上运动,且
上运动,且![]() 为等腰三角形时,求此时
为等腰三角形时,求此时![]() 的值;
的值;
(4)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 内接于⊙O,∠B=60°,CD 是⊙O 的直径,点 P 是 CD 延长线上的一点且 AP=AC.

(1)求证:PA 是⊙O 的切线;
(2)若![]() ,
,![]() ,求⊙O的半径
,求⊙O的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县第一届运动会需购买A,B两种奖品,若购买A种奖品4件和B种奖品3件,共需85元;若购买A种奖品3件和B种奖品1件,共需45元.
(1)求A、B两种奖品的单价各是多少元?
(2)运动会组委会计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买总费用W元,写出W(元)与m(件)之间的函数关系式,求出自变量m的取值范围,并设计出购买总费用最少的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com