
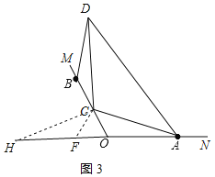
【题目】已知∠MON=120°,点A,B分别在ON,OM边上,且OA=OB,点C在线段OB上(不与点O,B重合),连接CA.将射线CA绕点C逆时针旋转120°得到射线CA′,将射线BO绕点B逆时针旋转150°与射线CA′交于点D.
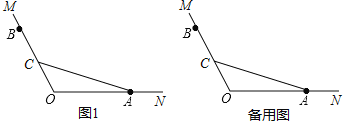
(1)根据题意补全图1;
(2)求证:
①∠OAC=∠DCB;
②CD=CA(提示:可以在OA上截取OE=OC,连接CE);
(3)点H在线段AO的延长线上,当线段OH,OC,OA满足什么等量关系时,对于任意的点C都有∠DCH=2∠DAH,写出你的猜想并证明.
【答案】(1)见解析;(2)①见解析;②见解析;(3)猜想OH﹣OC=OA时,对于任意的点C都有∠DCH=2∠DAH;理由见解析
【解析】
(1)根据题意即可补全图形;
(2)①由旋转得∠ACD=120°,由三角形内角和得出∠DCB+∠ACO=60°,∠OAC+∠ACO=60°,即可得出结论;
②在OA上截取OE=OC,连接CE,则∠OEC=∠OCE=![]() (180°﹣∠MON)=30°,∠AEC=150°,得出∠AEC=∠CBD,易证AE=BC,由ASA证得△AEC≌△CBD,即可得出结论;
(180°﹣∠MON)=30°,∠AEC=150°,得出∠AEC=∠CBD,易证AE=BC,由ASA证得△AEC≌△CBD,即可得出结论;
(3)猜想OH﹣OC=OA时,对于任意的点C都有∠DCH=2∠DAH,在OH上截取OF=OC,连接CF、CH,则FH=OA,∠COF=180°﹣∠MON=60°,得出△OFC 是等边三角形,则CF=OC,∠CFH=∠COA=120°,由SAS证得△CFH≌△COA,得出∠H=∠OAC,由三角形外角性质得出∠BCH=∠COF+∠H=60°+∠H=60°+∠OAC,则∠DCH=60°+∠H+∠DCB=60°+2∠OAC,由CA=CD,∠ACD=120°,得出∠CAD=30°,即可得出∠DCH=2∠DAH.
解:(1)根据题意补全图形,如图1所示:
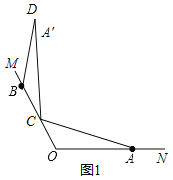
(2)证明:①由旋转得:∠ACD=120°,
∴∠DCB+∠ACO=180°﹣120°=60°,
∵∠MON=120°,
∴∠OAC+∠ACO=180°﹣120°=60°,
∴∠OAC=∠DCB;
②在OA上截取OE=OC,连接CE,如图2所示:
则∠OEC=∠OCE=![]() (180°﹣∠MON)=
(180°﹣∠MON)=![]() (180°﹣120°)=30°,
(180°﹣120°)=30°,
∴∠AEC=180°﹣∠OEC=180°﹣30°=150°,
由旋转得:∠CBD=150°,
∴∠AEC=∠CBD,
∵OA=OB,OE=OC,
∴AE=BC,在△AEC和△CBD中,
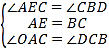 ,
,
∴△AEC≌△CBD(ASA),
∴CD=CA;
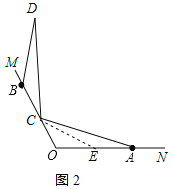
(3)解:猜想OH﹣OC=OA时,对于任意的点C都有∠DCH=2∠DAH;理由如下:
在OH上截取OF=OC,连接CF、CH,如图3所示:
则FH=OA,∠COF=180°﹣∠MON=180°﹣120°=60°,
∴△OFC 是等边三角形,
∴CF=OC,∠CFH=∠COA=120°,
在△CFH和△COA中,
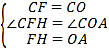 ,
,
∴△CFH≌△COA(SAS),
∴∠H=∠OAC,
∴∠BCH=∠COF+∠H=60°+∠H=60°+∠OAC,
∴∠DCH=60°+∠H+∠DCB=60°+2∠OAC,
∵CA=CD,∠ACD=120°,
∴∠CAD=30°,
∴∠DCH=2(∠CAD+∠OAC)=2∠DAH.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形 ABCD 中, AC 平分 ∠ DAB , ∠ ADC= ∠ ACB=90° , E 为 AB 的中点,连接 CE , DE . AC 与 DE 相交于点 F .
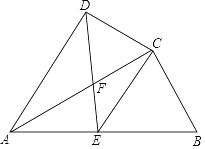
(1)求证: △ ADF ∽△ CEF ;
(2)若 AD=4 , AB=6 ,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=2,BC=4,点D、E分别是边BC、AB的中点,将△BDE绕着点B旋转,点D、E旋转后的对应点分别为点D′、E′,当直线D′E′经过点A时,线段CD′的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O直径,CD为⊙O的切线,C为切点,过A作CD的垂线,垂足为D.
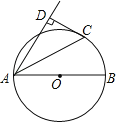
(1)求证:AC平分∠BAD;
(2)若⊙O半径为5,CD=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
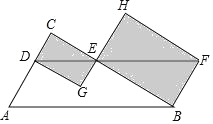
【题目】如图,在Rt△ABC中,∠C=90°,BC=4,BA=5,点D在边AC上的一动点,过点D作DE∥AB交边BC于点E,过点B作BF⊥BC交DE的延长线于点F,分别以DE,EF为对角线画矩形CDGE和矩形HEBF,则在D从A到C的运动过程中,当矩形CDGE和矩形HEBF的面积和最小时,则EF的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图与探究:
如图,△ABC中,AB=AC.

(1)作图:①画线段BC的垂直平分线l,设l与BC边交于点H;
②在射线HA上画点D,使AD=AB,连接BD. (不写作法,保留作图痕迹)
(2)探究:∠D与∠C有怎样的数量关系? 并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
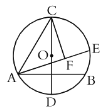
【题目】如图,在半径为4的![]() 中,
中,![]() 为直径,弦
为直径,弦![]() 且过半径
且过半径![]() 的中点,
的中点,![]() 为
为![]() 上一动点,
上一动点,![]() 于点
于点![]() ,即点
,即点![]() 在以
在以![]() 为直径的圆上,当
为直径的圆上,当![]() 从点
从点![]() 出发顺时针运动到点
出发顺时针运动到点![]() 时,点
时,点![]() 所经过的路径长为( )
所经过的路径长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶,甲车先到B地,停车1小时按原速度匀速返回,直到两车相遇.乙车速度是60千米/时,如图是两车之间的距离y(干米)与乙车行驶时间x(小时)之间的函数图象,则下列说法正确的是( )
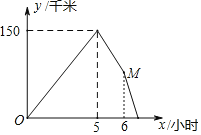
A.A、B两地相距150千米
B.甲车速度是100千米/时
C.乙车从出发到与甲车相遇共用![]() 小时
小时
D.点M的纵坐标为90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一节数学活动课上,王老师将本班学生身高数据(精确到1厘米)出示给大家,要求同学们各自独立绘制一幅频数分布直方图,甲绘制的如图①所示,乙绘制的如图②所示,经王老师批改,甲绘制的图是正确的,乙在数据整理与绘图过程中均有个别错误.
(1)写出乙同学在数据整理或绘图过程中的错误(写出一个即可);
(2)甲同学在数据整理后若用扇形统计图表示,则159.5﹣164.5这一部分所对应的扇形圆心角的度数为 ;
(3)该班学生的身高数据的中位数是 ;
(4)假设身高在169.5﹣174.5范围的5名同学中,有2名女同学,班主任老师想在这5名同学中选出2名同学作为本班的正、副旗手,那么恰好选中一名男同学和一名女同学当正,副旗手的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com