
【题目】如图,四边形 ABCD 中, AC 平分 ∠ DAB , ∠ ADC= ∠ ACB=90° , E 为 AB 的中点,连接 CE , DE . AC 与 DE 相交于点 F .
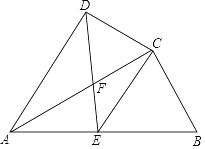
(1)求证: △ ADF ∽△ CEF ;
(2)若 AD=4 , AB=6 ,求 ![]() 的值.
的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)由角平分线的定义证明 ∠ DAC= ∠ CAB ,根据直角三角形斜边上的中线等于斜边的一半及等边对等角,证明 ∠ DAC= ∠ ECA ,得到 CE ∥ AD ,进而得到 △ ADF ∽△ CEF ;
(2)由△ AFD ∽△ CFE ;根据相似三角形的性质得出 AD ∶CE=AF :CF ;进而得出答案.
(1)证明: ∵ AC 平分 ∠ DAB ,
∴∠ DAC= ∠ CAB ,
∵ E 为 AB 的中点,
∴ CE=![]() AB=AE ,
AB=AE ,
∴∠ EAC= ∠ ECA ;
∵∠ DAC= ∠ CAB ,
∴∠ DAC= ∠ ECA ,
∴CE∥AD
∴△ ADF ∽△ CEF ,
(2)∵△ AFD ∽△ CFE ,
∴ AD∶ CE=AF ∶CF ;
∵ CE=![]() AB=3 , AD=4 ,
AB=3 , AD=4 ,
∴ ![]()
∴ ![]()
∴![]() =
=![]()


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
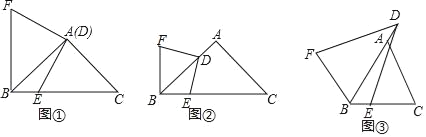
【题目】观察猜想:(1)如图①,在Rt△ABC中,∠BAC=90°,AB=AC=3,点D与点A重合,点E在边BC上,连接DE,将线段DE绕点D顺时针旋转90°得到线段DF,连接BF,BE与BF的位置关系是 ,BE+BF= ;
探究证明:(2)在(1)中,如果将点D沿AB方向移动,使AD=1,其余条件不变,如图②,判断BE与BF的位置关系,并求BE+BF的值,请写出你的理由或计算过程;
拓展延伸:(3)如图③,在△ABC中,AB=AC,∠BAC=a,点D在边BA的延长线上,BD=n,连接DE,将线段DE绕着点D顺时针旋转,旋转角∠EDF=a,连接BF,则BE+BF的值是多少?请用含有n,a的式子直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
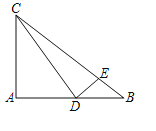
【题目】在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB边上一动点(点D与点A、B不重合),联结CD,过点D作DE⊥DC交边BC于点E.
(1)如图,当ED=EB时,求AD的长;
(2)设AD=x,BE=y,求y关于x的函数解析式并写出函数定义域;
(3)把△BCD沿直线CD翻折得△CDB',联结AB',当△CAB'是等腰三角形时,直接写出AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为切实加强中小学生交通安全宣传教育,让学生真正知危险、会避险,郑州市某中学开展了“交通安全进校园”系列活动.为了解七、八年级学生对交通安全知识的掌握情况,对七、八年级学生进行了测试,现从两年级中各随机抽取20名学生的测试成绩(百分制)进行整理、描述和分析(成绩不低于90分为优秀).
测试成绩(百分制)如下:
七年级:52,78,82,86,77,83,92,87,72,81,93,98,81,69,87,86,80,81,82,94
八年级:87,77,90,79,93,83,88,84,82,94,86,88,57,68,89,59,81,90,88,95
分组整理,描述数据
分组 | 七年级 | 八年级 | ||
画“正”计数 | 频数 | 画“正”计数 | 频数 | |
| 一 | 1 |
| 2 |
| 一 | 1 | 一 | 1 |
|
|
| 2 | |
|
| 正正 | 10 | |
|
| 4 | 正 | 5 |
七、八年级抽取学生的测试成绩统计表
年级 | 平均数 | 中位数 | 众数 | 优秀率 |
七年级 | 82 |
| 81 | 20% |
八年级 | 82.5 | 86.5 |
| 25% |
根据以上信息,回答下列问题:
(1)表中![]() __________,
__________,![]() __________,
__________,![]() __________,
__________,![]()
(2)若该校七年级270人和八年级280人参加了此次测试,估计参加此次测试成绩优秀的学生人数;
(3)根据以上数据,你认为该校七、八年级哪个年级学生掌握交通安全知识较好?并说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 △ ABC 中,∠ ACB=90° ,AC=BC=2 .E , F 分别是射线 AC 、CB 上的动点,且 AE=BF , EF 与 AB 交于点 G ,EH⊥ AB 于点 H ,设 AE=x ,GH=y ,下面能够反映 y 与 x 之间函数关系的图象是( )
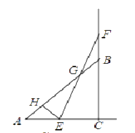
A.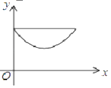 B.
B.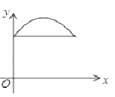 C.
C.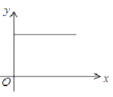 D.
D.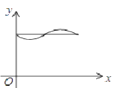
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富居民的文化生活.某社区开展跳舞、绘画、游泳、唱歌等活动来让居民娱乐.为了解居民对跳舞、绘画、游泳、唱歌这四种活动(以下分别用![]() ,
,![]() ,
,![]() ,
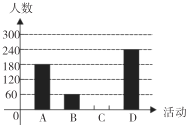
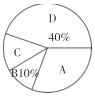
,![]() 表示这四种不同活动)的喜爱情况,在“五一”劳动节期间对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图.请根据以上信息回答:
表示这四种不同活动)的喜爱情况,在“五一”劳动节期间对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图.请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将不完整的条形图补充完整;
(3)若居民区有8000人,请估计爱唱歌的人数?
(4)在“五—”劳动节期间,该社区针对跳舞、绘画、游泳、唱歌起带头作用的居民各选举一名进行奖励,同时随机抽取两人进行现场展示,请用列表或画树状图法求恰好选中跳舞和绘画的概率.(跳舞、绘画、游泳、唱歌分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示)
表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MON=120°,点A,B分别在ON,OM边上,且OA=OB,点C在线段OB上(不与点O,B重合),连接CA.将射线CA绕点C逆时针旋转120°得到射线CA′,将射线BO绕点B逆时针旋转150°与射线CA′交于点D.
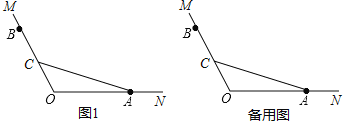
(1)根据题意补全图1;
(2)求证:
①∠OAC=∠DCB;
②CD=CA(提示:可以在OA上截取OE=OC,连接CE);
(3)点H在线段AO的延长线上,当线段OH,OC,OA满足什么等量关系时,对于任意的点C都有∠DCH=2∠DAH,写出你的猜想并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com