
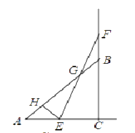
【题目】如图,在 △ ABC 中,∠ ACB=90° ,AC=BC=2 .E , F 分别是射线 AC 、CB 上的动点,且 AE=BF , EF 与 AB 交于点 G ,EH⊥ AB 于点 H ,设 AE=x ,GH=y ,下面能够反映 y 与 x 之间函数关系的图象是( )
A.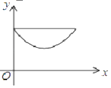 B.
B.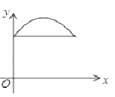 C.
C.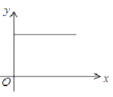 D.
D.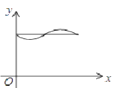
【答案】C
【解析】
先判断出 △ ABC 是等腰直角三角形,再判断出 △ AHE 是等腰直角三角形,然后根据勾股定理计算出 AB 、 AH 的长度,过点 B 作 BD ∥ AC 交 EF 于点 D ,然后利用平行线分线段成比例得出 B D:A E = B G:A G,B F:F C = B D:E C ,再表示出BD ,然后求出 BG 的长度,最后根据GH=AB﹣AH -BG ,代入数据就可以得出 y 关于 x 的函数关系式,再根据函数相应的图像解答.
解: ∵∠ ACB=90° , AC=BC=2 ,
∴△ABC是等腰直角三角形,
∴ AB=![]() , ∠ A=45° ,
, ∠ A=45° ,
∵ EH ⊥ AB 于点 H ,
∴△AHE是等腰直角三角形,
∵AC=BC=2
∴ AH=![]() AE=
AE=![]() x ,
x ,
过点 B作 BD∥AC交EF于点 D ,
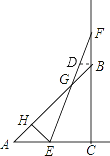
则
![]()
∴![]()
![]()
∴![]() =
=![]()
整理得, ![]()
解得, BG=![]() -
-![]() x ,
x ,
根据图形,GH=AB﹣AH﹣BG ,
=2![]() ﹣
﹣![]() x-(
x-(![]() -
-![]() x),
x),
=2![]() ﹣
﹣![]() x-
x-![]() +
+![]() x
x
=![]()
即 y=/span>![]() ,是一条平行于 x 轴的直线.
,是一条平行于 x 轴的直线.
故选: C ,


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
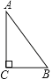
【题目】如图,在△ABC 中,∠C=90°,AB=10cm,BC=6cm,动点 P 从点 C 出发,沿 C﹣A﹣B﹣C 运动,速度为 2cm/s,动点 Q 从点 C 出发,沿 C﹣B﹣A﹣C 运动,速度为![]() cm/s,两点相遇时停止.这一过程中 P,Q 两点之间的距离 y 与时间 t 之间的关系的大致图象是( )
cm/s,两点相遇时停止.这一过程中 P,Q 两点之间的距离 y 与时间 t 之间的关系的大致图象是( )
A.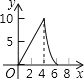 B.
B.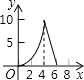 C.
C.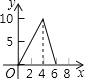 D.
D.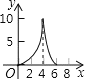
查看答案和解析>>
科目:初中数学 来源: 题型:
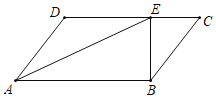
【题目】如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.
(1)求BC的长;
(2)若∠CBE=36°,求∠ADC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“穿越千古帝乡·感悟盛世汉风”,为拓宽同学们的视野,体验汉文化,我校七年级赴襄阳研学旅行.安排住宿时,为了安全考虑,学校包租一栋旅馆,若4人一间房,还有76人无法入住,若5人一间房,还有一间房空2个床位.
(1)求该旅馆的房间数和我校七年级研学人数;
(2)为保证顺利出行,学校共租了10辆客车,已知甲种型号客车载客量为45人/辆,乙种型号客车载客量为30人/辆,问:当甲种型号的客车至少租多少辆才能满足出行要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了积极助力脱贫攻坚工作,如期打赢脱贫攻坚战,某驻村干部带领村民种植草莓,在每年成熟期都会吸引很多人到果园去采摘.现有甲、乙两家果园可供采摘,这两家草莓的品质相同,售价均为每千克30元,但是两家果园的采摘方案不同:
甲果园:每人需购买20元的门票一张,采摘的草莓按6折优惠;
乙果园:不需要购买门票,采摘的草莓按售价付款不优惠.
设小明和爸爸妈妈三个人采摘的草莓数量为![]() 千克,在甲、乙果园采摘所需总费用分别为
千克,在甲、乙果园采摘所需总费用分别为![]() 、
、![]() 元,其函数图象如图所示.
元,其函数图象如图所示.

(1)分别写出![]() 、
、![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)请求出图中点![]() 的坐标;
的坐标;
(3)请根据函数图象,直接写出小明一家选择哪家果园采摘更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ABCD 中, AC 平分 ∠ DAB , ∠ ADC= ∠ ACB=90° , E 为 AB 的中点,连接 CE , DE . AC 与 DE 相交于点 F .
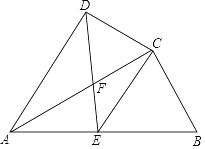
(1)求证: △ ADF ∽△ CEF ;
(2)若 AD=4 , AB=6 ,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的商品的市场指导价为每件150元,公司的实际销售价格可以浮动![]() 个百分点[即销售价格
个百分点[即销售价格![]() ],经过市场调研发现,这种商品的日销售量
],经过市场调研发现,这种商品的日销售量![]() (件)与销售价格浮动的百分点
(件)与销售价格浮动的百分点![]() 之间的函数关系如下:
之间的函数关系如下:
浮动 | 0 | 1 | 2 | 3 | … |
销售量 | 24 | 22 | 20 | 18 | … |
若该公司按浮动![]() 个百分点的价格出售,每件商品仍可获利10%.
个百分点的价格出售,每件商品仍可获利10%.
(1)求该公司生产每件商品的成本为多少元?
(2)当实际销售价格定为多少元时,日销售利润为660元?[说明:日销售利润![]() (销售价格
(销售价格![]() 成本)
成本)![]() 日销售量];
日销售量];
(3)该公司决定每销售一件商品就捐赠![]() 元利润(
元利润(![]() )给希望工程,公司通过销售记录发现,当价格浮动的百分点大于
)给希望工程,公司通过销售记录发现,当价格浮动的百分点大于![]() 时,扣除捐赠后的日销售利润随
时,扣除捐赠后的日销售利润随![]() 的增大而减小,直接写出
的增大而减小,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=4,BA=5,点D在边AC上的一动点,过点D作DE∥AB交边BC于点E,过点B作BF⊥BC交DE的延长线于点F,分别以DE,EF为对角线画矩形CDGE和矩形HEBF,则在D从A到C的运动过程中,当矩形CDGE和矩形HEBF的面积和最小时,则EF的长度为_____.
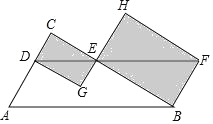
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com