
【题目】如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.
(1)求BC的长;
(2)若∠CBE=36°,求∠ADC.
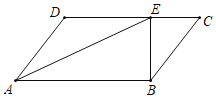
【答案】(1)BC=10;(2)126°.
【解析】
(1)依据DC∥AB,可得∠DEA=∠EAB,依据AE平分∠DAB,可得∠DAE=∠EAB,再根据∠DAE=∠DEA,即可得到AD=DE=10,进而得出BC=10;
(2)依据勾股定理的逆定理即可得出∠BEC=90°,再根据三角形内角和定理得出∠C的度数,进而得到∠ADC的度数.
解:(1)∵四边形ABCD是平行四边形,
∴AD=BC,DC∥AB,
∴∠DEA=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠DAE=∠DEA,
∴AD=DE=10,
∴BC=10;
(2)∵CE=6,BE=8,BC=10,
∴CE2+BE2=62+82=100=BC2,
∴△BCE是直角三角形,且∠BEC=90°,
∴∠C=90°﹣∠CBE=90°﹣36°=54°,
∵AD∥BC,
∴∠D=180°﹣∠C=180°﹣54°=126°.


科目:初中数学 来源: 题型:
【题目】A、B、C三瓶不同浓度的酒精,A瓶内有酒精2kg,浓度x%,B瓶有酒精3kg,浓度y%,C瓶有酒精5kg,浓度z%,从A瓶中倒出10%,B瓶中倒出20%,C瓶中倒出24%,混合后测得浓度33.5%,将混合后的溶液倒回瓶中,使它们恢复原来的质量,再从A瓶倒出30%,B瓶倒出30%,C瓶倒出30%,混合后测得浓度为31.5%,测量发现![]() ,
,![]() ,
,![]() ,且x、y、z均为整数,则把起初A、B两瓶酒精全部混合后的浓度为______.
,且x、y、z均为整数,则把起初A、B两瓶酒精全部混合后的浓度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿DF直线折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则OM的长为________.
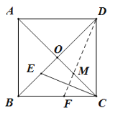
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+(m﹣2)x+3(m+1)与x轴交于AB两点(A在B左侧),与y轴正半轴交于点C.
(1)当m≠﹣4时,说明这个二次函数的图象与x轴必有两个交点;
(2)若OAOB=6,求点C的坐标;
(3)在(2)的条件下,在x轴下方的抛物线上找一点P,使S△PAC的面积为15,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上一点(不与点
边上一点(不与点![]() ,
,![]() 重合),将线段
重合),将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,则:
,则:
(1)①![]() 的度数是 ;②线段
的度数是 ;②线段![]() ,
,![]() ,
,![]() 之间的数量关系是 ;
之间的数量关系是 ;
(2)如图②,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上一点(不与点
边上一点(不与点![]() ,
,![]() 重合),将线段
重合),将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,请判断线段
,请判断线段![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)如图②,![]() 与
与![]() 交于点
交于点![]() ,在(2)条件下,若
,在(2)条件下,若![]() ,求
,求![]() 的最小值.
的最小值.
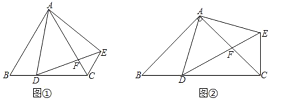
查看答案和解析>>
科目:初中数学 来源: 题型:
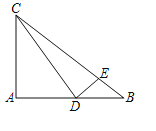
【题目】在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB边上一动点(点D与点A、B不重合),联结CD,过点D作DE⊥DC交边BC于点E.
(1)如图,当ED=EB时,求AD的长;
(2)设AD=x,BE=y,求y关于x的函数解析式并写出函数定义域;
(3)把△BCD沿直线CD翻折得△CDB',联结AB',当△CAB'是等腰三角形时,直接写出AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以
.以![]() 点为中心,顺时针旋转矩形
点为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() ,记旋转角为
,记旋转角为![]() .
.
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
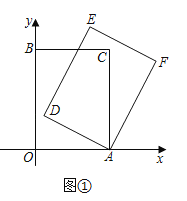
(2)如图②,当点![]() 落在
落在![]() 的延长线上时,求点
的延长线上时,求点![]() 的坐标;
的坐标;

(3)当点![]() 落在线段
落在线段![]() 上时,求点
上时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
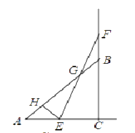
【题目】如图,在 △ ABC 中,∠ ACB=90° ,AC=BC=2 .E , F 分别是射线 AC 、CB 上的动点,且 AE=BF , EF 与 AB 交于点 G ,EH⊥ AB 于点 H ,设 AE=x ,GH=y ,下面能够反映 y 与 x 之间函数关系的图象是( )
A.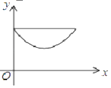 B.
B.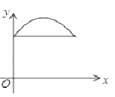 C.
C.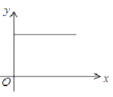 D.
D.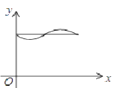
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△OA1B1是等边三角形,点B1的坐标是(2,0),反比例函数y=![]() 的图象经过点A1.
的图象经过点A1.
(1)求反比例函数的解析式.
(2)如图,以B1为顶点作等边三角形B1A2B2,使点B2在x轴上,点A2在反比例函数y=![]() 的图象上.若要使点B2在反比例函数y=
的图象上.若要使点B2在反比例函数y=![]() 的图象上,需将△B1A2B2向上平移多少个单位长度?
的图象上,需将△B1A2B2向上平移多少个单位长度?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com