
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

【答案】(1)y=﹣x2﹣x+2; (2)(0,2)或(﹣1,2)或(![]() ,﹣2)或(
,﹣2)或(![]() ,﹣2);(3)1.
,﹣2);(3)1.
【解析】(1)把点A、C的坐标分别代入函数解析式,列出关于系数的方程组,通过解方程组求得系数的值;
(2)设M点坐标为(m,n),根据S△AOM=2S△BOC列出关于m的方程,解方程求出m的值,进而得到点P的坐标;
(3)先运用待定系数法求出直线AC的解析式为y=x+2,再设N点坐标为(x,x+2),则D点坐标为(x,-x2-x+2),然后用含x的代数式表示ND,根据二次函数的性质即可求出线段ND长度的最大值.
解:(1)A(﹣2,0),C(0,2)代入抛物线的解析式y=﹣x2+mx+n,
得![]() ,
,
解得![]() ,
,
∴抛物线的解析式为y=﹣x2﹣x+2.
(2)由(1)知,该抛物线的解析式为y=﹣x2﹣x+2,则易得B(1,0),设M(m,n)然后依据S△AOM=2S△BOC列方程可得:
![]() AO×|n|=2×
AO×|n|=2×![]() ×OB×OC,
×OB×OC,
∴![]() ×2×|﹣m2﹣m+2|=2,
×2×|﹣m2﹣m+2|=2,
∴m2+m=0或m2+m﹣4=0,
解得m=0或﹣1或![]() ,
,
∴符合条件的点M的坐标为:(0,2)或(﹣1,2)或(![]() ,﹣2)或(
,﹣2)或(![]() ,﹣2).
,﹣2).
(3)设直线AC的解析式为y=kx+b,将A(﹣2,0),C(0,2)代入
得到![]() ,解得
,解得![]() ,
,
∴直线AC的解析式为y=x+2,
设N(x,x+2)(﹣2≤x≤0),则D(x,﹣x2﹣x+2),
ND=(﹣x2﹣x+2)﹣(x+2)=﹣x2﹣2x=﹣(x+1)2+1,
∵﹣1<0,
∴xspan>=﹣1时,ND有最大值1.
∴ND的最大值为1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形 OABC 是矩形,点 B 的坐标为(4,3).
(1)直接写出A、C两点的坐标;
(2)平行于对角线AC的直线 m 从原点O出发,沿 x 轴正方向以每秒 1 个单位长度的速度运动,设直线 m 与矩形 OABC 的两边分别交于点M、N,设直线m运动的时间为t(秒).
①若 MN=![]() AC,求 t 的值;
AC,求 t 的值;
②设△OMN 的面积为S,当 t 为何值时,S=![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
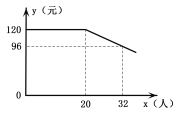
【题目】随着人们生活水平的提高,短途旅行日趋火爆.我市某旅行社推出“辽阳—葫芦岛海滨观光一日游”项目,团队人均报名费用y(元)与团队报名人数x(人)之间的函数关系如图所示,旅行社规定团队人均报名费用不能低于88元.旅行社收到的团队总报名费用为w(元).
(1)直接写出当x≥20时,y与x之间的函数关系式及自变量x的取值范围;
(2)儿童节当天旅行社收到某个团队的总报名费为3000元,报名旅游的人数是多少?
(3)当一个团队有多少人报名时,旅行社收到的总报名费最多?最多总报名费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]()
![]() 当m取何值时,这个方程有两个不相等的实根?
当m取何值时,这个方程有两个不相等的实根?
![]() 若方程的两根都是正数,求m的取值范围;
若方程的两根都是正数,求m的取值范围;
![]() 设
设![]() ,
,![]() 是这个方程的两个实数根,且
是这个方程的两个实数根,且![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
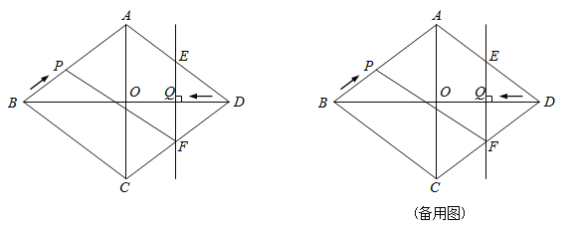
【题目】已知:如图,菱形ABCD中,对角线AC、BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
(1)当t为何值时,四边形APFD是平行四边形?
(2)设四边形APFE的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形APFE∶S菱形ABCD=17∶40?若存在,求出t的值,并求出此时P,E两点间的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工人打算用不锈钢条加工一个面积为0.8平方米的矩形模具.假设模具的长与宽分别为x米和y米.
(1)你能写出y与x之间的函数解析式吗?
(2)变量y与x是什么函数关系?
(3)已知这种不锈钢条每米6元,若想使模具的长比宽多1.6米,则加工这个模具共需花多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com