
【题目】如图,在平面直角坐标系中,四边形 OABC 是矩形,点 B 的坐标为(4,3).
(1)直接写出A、C两点的坐标;
(2)平行于对角线AC的直线 m 从原点O出发,沿 x 轴正方向以每秒 1 个单位长度的速度运动,设直线 m 与矩形 OABC 的两边分别交于点M、N,设直线m运动的时间为t(秒).
①若 MN=![]() AC,求 t 的值;
AC,求 t 的值;
②设△OMN 的面积为S,当 t 为何值时,S=![]() .
.

【答案】(1)A(4,0),C(0,3);(2)①t=2 或 6;②t=2 或 4+2![]()
【解析】
(1)因为四边形OABC是矩形且点B的坐标为(4,3),所以可知,OA=CB=4,OC=AB=3,故可知A、C两点的坐标;
(2)①可以分为两种情况:当M、N分别在OA、OC上时,可证明△OMN∽△OAC,由题意可求得OM的长,即可求得t的值;当M、N分别在AB、BC上时,可证明△BMN∽△BAC,由题意可求得BM的长,即可由相似三角形的性质求得t的值,综合以上两种情况即是要求的t值.
②可以分为两种情况:当M、N分别在OA、OC上时,可证明△OMN∽△OAC,由题意可求得OM、ON的长,即可求得面积的表达式,再由面积为![]() 可得t的值;当M、N分别在AB、BC上时,由△DAM∽△AOC,可得AM,由△BMN∽△BAC,可得BN,即可得BM、CN,由S=矩形OABC的面积-Rt△OAM的面积-Rt△MBN的面积-Rt△NCO的面积,可得关于t的表达式,再由面积为
可得t的值;当M、N分别在AB、BC上时,由△DAM∽△AOC,可得AM,由△BMN∽△BAC,可得BN,即可得BM、CN,由S=矩形OABC的面积-Rt△OAM的面积-Rt△MBN的面积-Rt△NCO的面积,可得关于t的表达式,再由面积为![]() 可得t的值,综合以上两种情况即是要求的t值.
可得t的值,综合以上两种情况即是要求的t值.
解:(1)A(4,0),C(0,3);
(2)①x 轴正方向以每秒 1 个单位长度的速度运动,直线 m 运动的时间为 t , 可以分为两种情况:
当 M、N 分别在 OA、OC 上时,如下图所示:
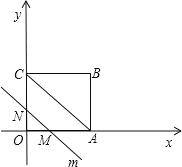
∵直线 m 平行于对角线 AC
∴△OMN∽△OAC
∴![]() =
=![]() =
=![]()
∴t=2;
当 M、N 分别在 AB、BC 上时,如下图所示:
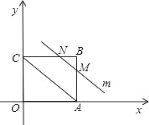
∵直线 m 平行于对角线 AC
∴△BMN∽△BAC
∴![]() =
=![]() =
= ![]() =
= ![]()
∴t=6
综上所述,当 t=2 或 6 时,MN=![]() AC
AC
得![]()
②当 0<t≤4 时,OM=t,△OMN∽△OAC,得 ![]() ,
,
∴ON=![]() t,S=
t,S=![]() t2=
t2=![]()
∴t=2;
当 4<t<8 时,
如图,∵OD=t,∴AD=t﹣4.

由△DAM∽△AOC,可得 AM=![]() (t﹣4)
(t﹣4)
∴BM=6﹣![]() t.
t.
由△BMN∽△BAC,可得 BN=![]() BM=8﹣t
BM=8﹣t
∴CN=t﹣4
S=矩形 OABC 的面积﹣Rt△OAM 的面积﹣Rt△MBN 的面积﹣Rt△NCO 的面积
=12﹣![]() ﹣
﹣![]() (8﹣t)(6﹣
(8﹣t)(6﹣![]() t)﹣
t)﹣![]()
=﹣![]() t2+3t,
t2+3t,
∴﹣![]() t2+3t=
t2+3t=![]()
解得:t=4±2![]()
∴t=4+2![]()
故当 t=2 或 4+2![]() 时,△OMN 的面积 S=
时,△OMN 的面积 S=![]() .
.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣![]() x>
x>![]() 的解集;
的解集;
(3)将直线l1:y=- ![]() x沿y向上平移后的直线l2与反比例函数y=
x沿y向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
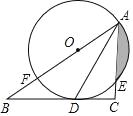
【题目】如图,在Rt△ABC中,![]() ,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生的课余生活,拓展学生的视野,某学校开设了特色选修课程.本学期该校共开设A、B、C三类课程,如下表所示.

(1)若小明从A类课程中随机选择一门课程,则他恰好选中“合唱”的概率是 .
(2)若小明分别从B类课程和C类课程中各随机选择一门课程,求他恰好选中“汉字的故事”和“乒乓球”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(数学概念)
若等边三角形的三个顶点D、E、F分别在△ABC的三条边上,我们称等边三角形DEF是△ABC的内接正三角形.
(概念辨析)
(1)下列图中△DEF均为等边三角形,则满足△DEF是△ABC的内接正三角形的是 .
A.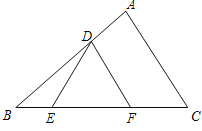 B.
B.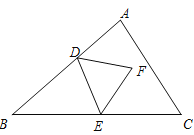
C.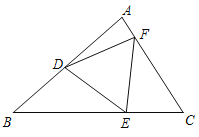
(操作验证)
(2)如图①.在△ABC中,∠B=60°,D为边AB上一定点(BC>BD),DE=DB,EM平分∠DEC,交边AC于点M,△DME的外接圆与边BC的另一个交点为N.
求证:△DMN是△ABC的内接正三角形.
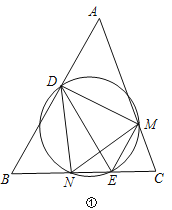
(知识应用)
(3)如图②.在△ABC中,∠B=60°,∠A=45°,BC=2,D是边AB上的动点,若边BC上存在一点E,使得以DE为边的等边三角形DEF是△ABC的内接正三角形.设△DEF的外接圆⊙O与边BC的另一个交点为K,则DK的最大值为 ,最小值为 .
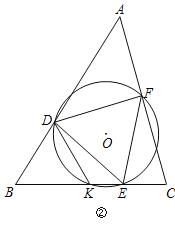
查看答案和解析>>
科目:初中数学 来源: 题型:
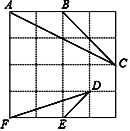
【题目】如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
⑴填空:∠ABC= °,AC= ;
⑵判断:△ABC与△DEF是否相似,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
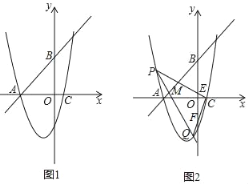
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=x+4分别交x轴、y轴于A、B两点,抛物线y=x2+mx﹣4经过点A,和x轴的另一个交点为C.
(1)求抛物线的解析式;
(2)如图1,点D是抛物线上的动点,且在第三象限,求△ABD面积的最大值;
(3)如图2,经过点M(﹣4,1)的直线交抛物线于点P、Q,连接CP、CQ分别交y轴于点E、F,求OEOF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
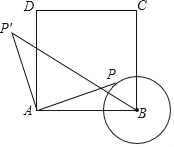
【题目】如图,正方形ABCD中,AB=3cm,以B为圆心,1cm长为半径画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针旋转90°至AP′,连接BP′.在点P移动的过程中,BP′长度的最小值为_____cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com