
【题目】如图,正方形ABCD中,AB=3cm,以B为圆心,1cm长为半径画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针旋转90°至AP′,连接BP′.在点P移动的过程中,BP′长度的最小值为_____cm.
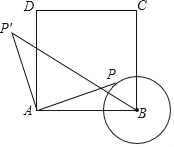
【答案】![]()
【解析】
通过画图发现,点P′的运动路线为以D为圆心,以1为半径的圆,可知:当P′在对角线BD上时,BP′最小,先证明△PAB≌△P′AD,则P′D=PB=1,再利用勾股定理求对角线BD的长,则得出BP′的长.
如图,
当P′在对角线BD上时,BP′最小,
连接BP,
由旋转得:AP=AP′,∠PAP′=90°,
∴∠PAB+∠BAP′=90°,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BAP′+∠DAP′=90°,
∴∠PAB=∠DAP′,
∴△PAB≌△P′AD,
∴P′D=PB=1,
在Rt△ABD中,∵AB=AD=3,
由勾股定理得:BD=![]() ,
,
∴BP′=BD-P′D=3![]() -1,
-1,
即BP′长度的最小值为(3![]() -1)cm.
-1)cm.
故答案为:(3![]() -1).
-1).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形 OABC 是矩形,点 B 的坐标为(4,3).
(1)直接写出A、C两点的坐标;
(2)平行于对角线AC的直线 m 从原点O出发,沿 x 轴正方向以每秒 1 个单位长度的速度运动,设直线 m 与矩形 OABC 的两边分别交于点M、N,设直线m运动的时间为t(秒).
①若 MN=![]() AC,求 t 的值;
AC,求 t 的值;
②设△OMN 的面积为S,当 t 为何值时,S=![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
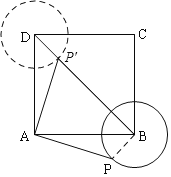
【题目】已知:如图,菱形ABCD中,对角线AC、BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
(1)当t为何值时,四边形APFD是平行四边形?
(2)设四边形APFE的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形APFE∶S菱形ABCD=17∶40?若存在,求出t的值,并求出此时P,E两点间的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个盒子中分别装有除颜色外都相同的小球,甲盒中装有两个球,分别为一个红球和一个绿球;乙盒中装有三个球,分别为两个绿球和一个红球;丙盒中装有两个球,分别为一个红球和一个绿球,从三个盒子中各随机取出一个小球
(1)请画树状图,列举所有可能出现的结果
(2)请直接写出事件“取出至少一个红球”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的A商品按每件100元出售,一天可售出128件.经过市场调查,发现这种商品的销售单价每降低1元,其日销量可增加8件.设该商品每件降价x元,商场一天可通过A商品获利润y元.
(1)求y与x之间的函数解析式(不必写出自变量x的取值范围)
(2)A商品销售单价为多少时,该商场每天通过A商品所获的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以△ABC的边AB,AC为边分别向外作正方形ABDE和正方形ACFG,连接EG,M为EG的中点,连接AM.
(1)如图1,∠BAC=90°,试判断AM与BC关系?
(2)如图2,∠BAC≠90°,图1中的结论是否成立?若不成立,说明理由;若成立,给出证明.
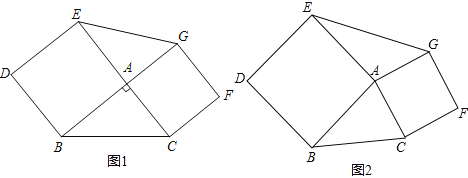
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工人打算用不锈钢条加工一个面积为0.8平方米的矩形模具.假设模具的长与宽分别为x米和y米.
(1)你能写出y与x之间的函数解析式吗?
(2)变量y与x是什么函数关系?
(3)已知这种不锈钢条每米6元,若想使模具的长比宽多1.6米,则加工这个模具共需花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
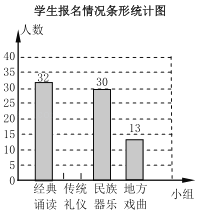
【题目】为推进“传统文化进校园”活动,某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图(每人只能选择一个小组):
(1)报名参加“民族器乐”课外活动小组的学生数占所有报名人数的30%,报名参加课外活动小组的学生共有______人,并将条形统计图补充完整;
(2)根据报名情况,学校决定从报名“地方戏曲”小组的甲、乙、丙三人中随机调整两人到“经典诵读”小组,甲、乙恰好都被调整到“经典诵读”小组的概率是多少?请用列表或画树状图的方法说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
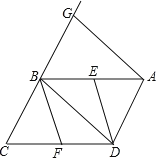
【题目】已知:如图,在平行四边形![]() 中,
中,![]() 分别为边
分别为边![]() 的中点,连接
的中点,连接![]() ,作
,作![]() 交
交![]() 的延长线于
的延长线于![]() .
.
(1)求证:![]() ;
;
(2)若四边形![]() 是矩形,则四边形
是矩形,则四边形![]() 是什么特殊四边形?证明你的结论.
是什么特殊四边形?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com