
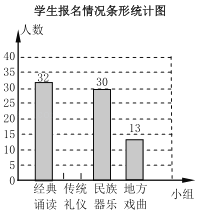
【题目】为推进“传统文化进校园”活动,某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图(每人只能选择一个小组):
(1)报名参加“民族器乐”课外活动小组的学生数占所有报名人数的30%,报名参加课外活动小组的学生共有______人,并将条形统计图补充完整;
(2)根据报名情况,学校决定从报名“地方戏曲”小组的甲、乙、丙三人中随机调整两人到“经典诵读”小组,甲、乙恰好都被调整到“经典诵读”小组的概率是多少?请用列表或画树状图的方法说明.
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
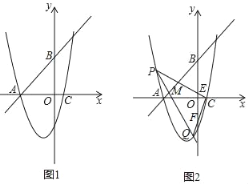
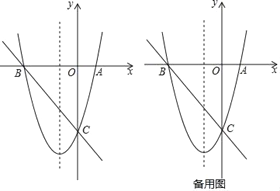
【题目】已知直线y=x+4分别交x轴、y轴于A、B两点,抛物线y=x2+mx﹣4经过点A,和x轴的另一个交点为C.
(1)求抛物线的解析式;
(2)如图1,点D是抛物线上的动点,且在第三象限,求△ABD面积的最大值;
(3)如图2,经过点M(﹣4,1)的直线交抛物线于点P、Q,连接CP、CQ分别交y轴于点E、F,求OEOF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
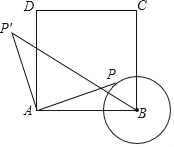
【题目】如图,正方形ABCD中,AB=3cm,以B为圆心,1cm长为半径画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针旋转90°至AP′,连接BP′.在点P移动的过程中,BP′长度的最小值为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
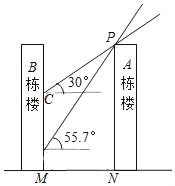
【题目】如图,某小区A栋楼在B栋楼的南侧,两楼高度均为90m,楼间距为MN.春分日正午,太阳光线与水平面所成的角为55.7°,A栋楼在B栋楼墙面上的影高为DM;冬至日正午,太阳光线与水平面所成的角为30°,A栋楼在B栋楼墙面上的影高为CM.已知CD=44.5m.
(1)求楼间距MN;
(2)若B号楼共30层,每层高均为3m,则点C位于第几层?(参考数据:tan30°≈0.58,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C.
x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C.
(1)求直线BC的解析式;
(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,在抛物线的对称轴上找一点P,使得△BFP的周长最小,请求出点F的坐标和点P的坐标;
(3)在(2)的条件下,是否存在这样的点Q(0,m),使得△BFQ为等腰三角形?如果有,请直接写出点Q的坐标;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )

A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于三角函数有如下的公式:
sin(α+β)=sinαcosβ+cosαsinβ①
cos(α+β)=cosαcosβ﹣sinαsinβ②
tan(α+β)=![]() ③
③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,如:
tan105°=tan(45°+60°)=![]() =﹣(2+
=﹣(2+![]() ).
).
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
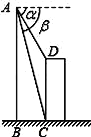
如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “任意画一个三角形,其内角和为![]() ”是随机事件;
”是随机事件;
B. 某种彩票的中奖率是![]() ,说明每买100张彩票,一定有1张中奖;
,说明每买100张彩票,一定有1张中奖;
C. “篮球队员在罚球线上投篮一次,投中”为随机事件;
D. 投掷一枚质地均匀的硬币100次,正面向上的次数一定是50次.
查看答案和解析>>
科目:初中数学 来源: 题型:
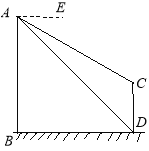
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com