
【题目】已知关于x的一元二次方程![]()
![]() 当m取何值时,这个方程有两个不相等的实根?
当m取何值时,这个方程有两个不相等的实根?
![]() 若方程的两根都是正数,求m的取值范围;
若方程的两根都是正数,求m的取值范围;
![]() 设
设![]() ,
,![]() 是这个方程的两个实数根,且
是这个方程的两个实数根,且![]() ,求m的值.
,求m的值.
【答案】(1)m<2;(2)m>1;(3)m=4.
【解析】
(1)令>0列式求解即可;
(2)令x1x2>0,结合(1)的结论求解即可;
(3)用含m的式子表示出x1x2与x12+x22的值,把所给代数式变形为1+x1x2=(x1+x2)2,代入x1x2与x12+x22的值即可求出m的值.
解:(1)∵△=(-2)2-4(m-1)=-4m+8>0,
∴m<2时,方程有两个不相等的实数根;
(2)设x1,x2是这个方程的两个实根,则x1>0,x2>0,
∴x1x2=m-1>0,
∴m>1,
∴方程的两根都是正数,m的取值范围是:1<m≤2;
(3)∵x1+x2=2,x1x2=m-1,
∴1-x1x2=x12+x22,
∴1+x1x2=(x1+x2)2,
∴1+m-1=22,
∴m=4.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC = 90°,BC = 1,AC =![]() .
.

(1)以点B为旋转中心,将△ABC沿逆时针方向旋转90°得到△A′BC′,请画出变换后的图形;
(2)求点A和点A′之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生的课余生活,拓展学生的视野,某学校开设了特色选修课程.本学期该校共开设A、B、C三类课程,如下表所示.

(1)若小明从A类课程中随机选择一门课程,则他恰好选中“合唱”的概率是 .
(2)若小明分别从B类课程和C类课程中各随机选择一门课程,求他恰好选中“汉字的故事”和“乒乓球”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
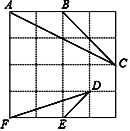
【题目】如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
⑴填空:∠ABC= °,AC= ;
⑵判断:△ABC与△DEF是否相似,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,An,分别过这些点做x轴的垂线与反比例函数y=![]() 的图象相交于点P1,P2,P3,P4,…Pn,再分别过P2,P3,P4,…Pn作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,…,PnBn﹣1⊥An﹣1Pn﹣1,垂足分别为B1,B2,B3,B4,…,Bn﹣1,连接P1P2,P2P3,P3P4,…,Pn﹣1Pn,得到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,…,Rt△Pn﹣1Bn﹣1Pn,则Rt△Pn﹣1Bn﹣1Pn的面积为_____.
的图象相交于点P1,P2,P3,P4,…Pn,再分别过P2,P3,P4,…Pn作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,…,PnBn﹣1⊥An﹣1Pn﹣1,垂足分别为B1,B2,B3,B4,…,Bn﹣1,连接P1P2,P2P3,P3P4,…,Pn﹣1Pn,得到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,…,Rt△Pn﹣1Bn﹣1Pn,则Rt△Pn﹣1Bn﹣1Pn的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
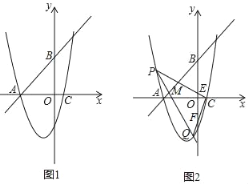
【题目】已知直线y=x+4分别交x轴、y轴于A、B两点,抛物线y=x2+mx﹣4经过点A,和x轴的另一个交点为C.
(1)求抛物线的解析式;
(2)如图1,点D是抛物线上的动点,且在第三象限,求△ABD面积的最大值;
(3)如图2,经过点M(﹣4,1)的直线交抛物线于点P、Q,连接CP、CQ分别交y轴于点E、F,求OEOF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
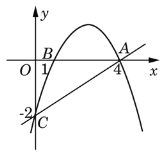
【题目】如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
(1)求出抛物线的解析式;
(2)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
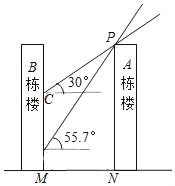
【题目】如图,某小区A栋楼在B栋楼的南侧,两楼高度均为90m,楼间距为MN.春分日正午,太阳光线与水平面所成的角为55.7°,A栋楼在B栋楼墙面上的影高为DM;冬至日正午,太阳光线与水平面所成的角为30°,A栋楼在B栋楼墙面上的影高为CM.已知CD=44.5m.
(1)求楼间距MN;
(2)若B号楼共30层,每层高均为3m,则点C位于第几层?(参考数据:tan30°≈0.58,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com