Question

如图，在△ABC中，4AB=5AC，AD为△ABC的角平分线，点E在BC的延长线上，EF⊥AD于点F，点G在AF上，FG=FD，连接EG交AC于点H．若点H是AC的中点，则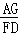的值为　 　．

 

 

Answer 1

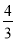
【解析】

试题分析：：已知AD为角平分线，则点D到AB、AC的距离相等，设为h．

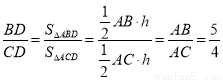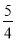∵，∴BD=CD．

如下图，延长AC，在AC的延长线上截取AM=AB，则有AC=4CM．连接DM．

在△ABD与△AMD中，

∴△ABD≌△AMD（SAS），

∴MD=BD=5m．

过点M作MN∥AD，交EG于点N，交DE于点K．

∵MN∥AD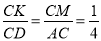，∴，∴CK=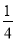CD，∴K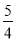D=CD．

∴MD=KD，即△DMK为等腰三角形，

∴∠DMK=∠DKM．

由题意，易知△EDG为等腰三角形，且∠1=∠2；

∵MN∥AD，∴∠3=∠4=∠1=∠2，

又∵∠DKM=∠3（对顶角）

∴∠DMK=∠4，

∴DM∥GN，

∴四边形DMNG为平行四边形，

∴MN=DG=2FD．

∵点H为AC中点，AC=4CM，∴．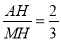

∵MN∥AD，

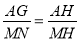∴，即，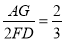

∴．

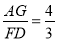考点：1、相似三角形的判定与性质；2、全等三角形的判定与性质；3、等腰三角形的判定与性质；4、平行四边形的判定与性质．