
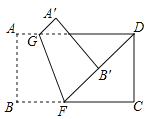
【题目】如图,一张矩形纸片![]() .点
.点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使
上,将纸片折叠,使![]() 落在射线
落在射线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() 分别落在点
分别落在点![]() 处,
处,
(1)若![]() ,则
,则![]() 的度数为 °;
的度数为 °;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;(2)3
;(2)3
【解析】
(1)根据折叠可得∠BFG=∠GFB′,再根据矩形的性质可得∠DFC=40°,从而∠BFG=70°即可得到结论;
(2) 首先求出GD=9-![]() =
=![]() ,由矩形的性质得出AD∥BC,BC=AD=9,由平行线的性质得出∠DGF=∠BFG,由翻折不变性可知,∠BFG=∠DFG,证出∠DFG=∠DGF,由等腰三角形的判定定理证出DF=DG=
,由矩形的性质得出AD∥BC,BC=AD=9,由平行线的性质得出∠DGF=∠BFG,由翻折不变性可知,∠BFG=∠DFG,证出∠DFG=∠DGF,由等腰三角形的判定定理证出DF=DG=![]() ,再由勾股定理求出CF,可得BF,再利用翻折不变性,可知FB′=FB,由此即可解决问题.
,再由勾股定理求出CF,可得BF,再利用翻折不变性,可知FB′=FB,由此即可解决问题.
(1)根据折叠可得∠BFG=∠GFB′,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DGF=∠BFG,∠ADF=∠DFC,
∵![]()
∴∠DFC=40°
∴∠BFD=140°
∴∠BFG=70°
∴∠DGF=70°;
(2)∵AG=![]() ,AD=9,
,AD=9,
∴GD=9-![]() =
=![]() ,
,
∵四边形ABCD是矩形,
∴AD∥BC,BC=AD=9,
∴∠DGF=∠BFG,
由翻折不变性可知,∠BFG=∠DFG,
∴∠DFG=∠DGF,
∴DF=DG=![]() ,
,
∵CD=AB=4,∠C=90°,
∴在Rt△CDF中,由勾股定理得: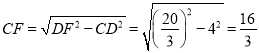 ,
,
∴BF=BC-CF=9-![]() ,
,
由翻折不变性可知,FB=FB′=![]() ,
,
∴B′D=DF-FB′=![]() -
-![]() =3.
=3.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让同学们了解自己的体育水平,八年级![]() 班的体育老师对全班
班的体育老师对全班![]() 名学生进行了一次体育模拟测试(得分均为整数),成绩满分为
名学生进行了一次体育模拟测试(得分均为整数),成绩满分为![]() 分,
分,![]() 班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
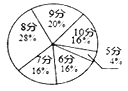
八年级![]() 班全体女生体育测试成绩分布扇形统计图
班全体女生体育测试成绩分布扇形统计图
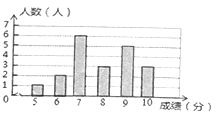
八年级全体男生体育测试成绩条形统计图
八年级![]() 班体育模拟测试成绩分析表
班体育模拟测试成绩分析表
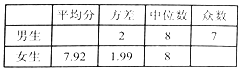
根据以上信息,解答下列问题:
(1)这个班共有男生 人,共有女生 人;
(2)补全八年级![]() 班体育模拟测试成绩分析表;
班体育模拟测试成绩分析表;
(3)你认为在这次体育测试中,![]() 班的男生队,女生队哪个表现更突出一些?并写出你的看法的理由.
班的男生队,女生队哪个表现更突出一些?并写出你的看法的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.
(1)当参加旅游的人数不超过10人时,人均收费为 元;
(2)如果该公司支付给旅行社3600元,那么参加这次旅游的人数是多少?
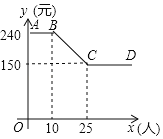
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①已知抛物线y=ax2﹣3ax﹣4a(a<0)的图象与x轴交于A、B两点(A在B的左侧),与y的正半轴交于点C,连结BC,二次函数的对称轴与x轴的交点为E.
(1)抛物线的对称轴与x轴的交点E坐标为_____,点A的坐标为_____;
(2)若以E为圆心的圆与y轴和直线BC都相切,试求出抛物线的解析式;
(3)在(2)的条件下,如图②Q(m,0)是x的正半轴上一点,过点Q作y轴的平行线,与直线BC交于点M,与抛物线交于点N,连结CN,将△CMN沿CN翻折,M的对应点为M′.在图②中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
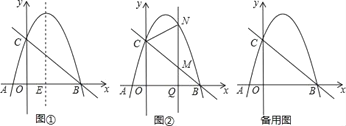
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张同学尝试运用课堂上学到的方法,自主研究函数![]() 的图像与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
的图像与性质.下面是小张同学在研究过程中遇到的几个问题,现由你来完成:
(1)函数y=![]() 的定义域是 ;
的定义域是 ;
(2)下表列出了![]() 与
与![]() 的几组对应值:
的几组对应值:
| … |
|
|
|
|
|
|
| 1 |
|
| … |
| … |
|
|
|
|
| 4 |
| 1 |
|
| … |
表中![]() 的值是 ;
的值是 ;
(3)如图,在平面直角坐标系![]() 中,描出以表中各组对应值为坐标的点,试由描出的点画出该函数的图像;
中,描出以表中各组对应值为坐标的点,试由描出的点画出该函数的图像;
(4)结合函数![]() 的图像,写出这个函数的性质: .(只需写一个)
的图像,写出这个函数的性质: .(只需写一个)
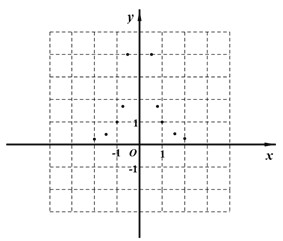
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民使用自来水按如下标准收费(水费按月缴纳):
户月用水量 | 单价 |
不超过 |
|
超过 |
|
超过 |
|
(1)当![]() 时,某用户一个月用了
时,某用户一个月用了![]() 水,求该用户这个月应缴纳的水费;
水,求该用户这个月应缴纳的水费;
(2)设某户月用水量为![]() 立方米,当
立方米,当![]() 时,求该用户应缴纳的水费(用含
时,求该用户应缴纳的水费(用含![]() 、
、![]() 的整式表示);
的整式表示);
(3)当![]() 时,甲、乙两用户一个月共用水
时,甲、乙两用户一个月共用水![]() .已知甲用户用水量超过了
.已知甲用户用水量超过了![]() ,设甲用户这个月用水如
,设甲用户这个月用水如,试求甲、乙两用户一个月共缴纳的水费.(用含
![]() 的整式表示)
的整式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com