
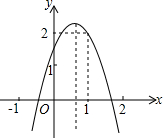
 如图,二次函数y=ax 2+bx+c(a≠0)的图象经过点(1,2),且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2.下列结论:①abc<0;②b<-2a;③b2+8a>4ac;④2a+c<0.其中正确的结论有( )
如图,二次函数y=ax 2+bx+c(a≠0)的图象经过点(1,2),且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2.下列结论:①abc<0;②b<-2a;③b2+8a>4ac;④2a+c<0.其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,根据对称轴在y轴的右侧,a,b异号,b>0,判断①;根据对称轴小于1,判断②;根据顶点的纵坐标大于2判断③,根据图象经过(1,2)和当x=-1时,y<0判断④.
解答 解:∵抛物线的开口向下,∴a<0,
∵抛物线与y轴的正半轴相交,∴c>0,
∵对称轴在y轴的右侧,a,b异号,∴b>0,
∴①abc<0,正确;
∵-$\frac{b}{2a}$<1,
∴②b<-2a,正确;
由于抛物线的顶点纵坐标大于2,即:$\frac{4ac-{b}^{2}}{4a}$>2,
由于a<0,所以4ac-b2<8a,即b2+8a>4ac,故③正确,
∵图象经过点(1,2),∴a+b+c=2,b=2-a-c,
当x=-1时,y<0,∴a-b+c<0,
2a+2c-2<0,2a+c<2-c,2-c>0,
∴④不一定正确
故选:C.
点评 本题考查了二次函数图象与系数的关系,二次函数y=ax2+bx+c系数符号的确定:
(1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0.
(2)b由对称轴和a的符号确定:由对称轴公式x=-$\frac{b}{2a}$判断符号.
(3)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0.
(4)b2-4ac由抛物线与x轴交点的个数确定:2个交点,b2-4ac>0;1个交点,b2-4ac=0;没有交点,b2-4ac<0.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛掷一枚质地均匀的硬币,落地后正面朝上 | |
| B. | 营山县8月份某一天的最低气温是-20℃ | |
| C. | 通常加热到100℃时,水沸腾 | |
| D. | 打开电视,正在播放节目《新闻联播》 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{6y=6x+6}\\{4x=7y+20}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{6x-6y=6}\\{4x=7y-20}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{6x+6=6y}\\{4x-4y=3y-20}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{6x-6=6y}\\{4x-4y=3y+20}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 150(1+x)2=450 | B. | 150(1+x)+150(1+x)2=450 | ||
| C. | 150(1+2x)2=450 | D. | 150(1+x)2=600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com