
 如图,已知A,B是线段MN上的两点,MN=8,MA=2,MB>2,以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M,N两点重合成一点C,构成△ABC,设AB=x,则x的取值范围是2<x<4,△ABC的最大面积为2$\sqrt{2}$.
如图,已知A,B是线段MN上的两点,MN=8,MA=2,MB>2,以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M,N两点重合成一点C,构成△ABC,设AB=x,则x的取值范围是2<x<4,△ABC的最大面积为2$\sqrt{2}$. 分析 ①表示出BN,再根据旋转的性质可得MA=AC,BN=BC,然后根据三角形的任意两边之和大于第三边和三角形的任意两边之差小于第三边列出不等式组求解即可;
②过点C作CD⊥AB于D,设CD=h,利用勾股定理表示出AD、BD,再根据BD=AB-AD列方程求出x2h2,然后求出△ABC的面积的平方,再根据二次函数的最值问题解答.
解答 解:①∵MN=8,MA=2,AB=x,
∴BN=8-2-x=6-x,
由旋转的性质得,MA=AC=2,BN=BC=6-x,
由三角形的三边关系得 $\left\{\begin{array}{l}{6-x-2<x}\\{6-x+2>x}\end{array}\right.$,
解不等式①得,x>2,
解不等式②得,x<4,
所以,x的取值范围是2<x<4;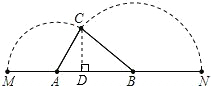
故答案为2<x<4.
②如图,过点C作CD⊥AB于D,设CD=h,
由勾股定理得,AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{{2}^{2}-{h}^{2}}$,
BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=$\sqrt{((6-x)^{2}-{h}^{2}}$,
∵BD=AB-AD,
∴$\sqrt{(6-x)^{2}-{h}^{2}}$=x-$\sqrt{{2}^{2}-{h}^{2}}$,
两边平方并整理得,x$\sqrt{{2}^{2}-{h}^{2}}$=6x-16,
两边平方整理得,x2h2=-32x2+192x-256,
∴S△ABC=$\frac{1}{2}$•AB•DC=$\frac{1}{2}$$\sqrt{-32{x}^{2}+192x-256}$=$\frac{1}{2}$$\sqrt{-32(x-3)^{2}+32}$,
∴x=3时,△ABC的面积最大,最大值为2$\sqrt{2}$.
故答案为2$\sqrt{2}$.
点评 本题考查了旋转的性质,三角形的三边关系,勾股定理,二次函数的最值问题,解题的关键是学会构建二次函数,利用二次函数的性质解决最值问题,属于中考常考题型.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
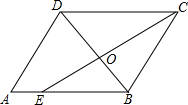 如图所示,在?ABCD中,CE是∠DCB的平分线,且交AB于E,DB与CE相交于O,已知AB=6,BC=4,则$\frac{OB}{DB}$等于( )
如图所示,在?ABCD中,CE是∠DCB的平分线,且交AB于E,DB与CE相交于O,已知AB=6,BC=4,则$\frac{OB}{DB}$等于( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{7}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com