
【题目】如图,矩形![]() 的中,
的中,![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别以
分别以![]() 、
、![]() 的速度从点
的速度从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 从点
从点![]() 向点
向点![]() 移动.
移动.
(1)若点![]() 从点
从点![]() 移动到点
移动到点![]() 停止,点
停止,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,问经过
同时出发,问经过![]() 时
时![]() 、
、![]() 两点之间的距离是多少
两点之间的距离是多少![]() ?
?
(2)若点![]() 从点
从点![]() 移动到点
移动到点![]() 停止,点
停止,点![]() 随之停止移动,点
随之停止移动,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,问经过多长时间
同时出发,问经过多长时间![]() 、
、![]() 两点之间的距离是
两点之间的距离是![]() ?
?
(3)若点![]() 沿着
沿着![]() 移动,点
移动,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 从点
从点![]() 移动到点
移动到点![]() 停止时,点
停止时,点![]() 随之也停止移动,试探求经过多长时间△
随之也停止移动,试探求经过多长时间△![]() 的面积为
的面积为![]() 2?
2?
【答案】![]() 经过
经过![]() 时
时![]() 、
、![]() 两点之间的距离是
两点之间的距离是![]() ;
;![]() 经过
经过![]() 或
或![]() 、
、![]() 两点之间的距离是
两点之间的距离是![]() ;
;![]() 经过
经过![]() 秒或
秒或![]() 秒
秒![]() 的面积为
的面积为![]() .
.
【解析】
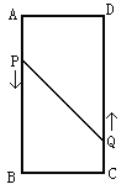
(1)作PE⊥CD于E,表示出PQ的长度,利用PE2+EQ2=PQ2列出方程求解即可;
(2)设x秒后,点P和点Q的距离是10cm.在Rt△PEQ中,根据勾股定理列出关于x的方程(16﹣5x)2=64,通过解方程即可求得x的值;
(3)分类讨论:①当点P在AB上时;②当点P在BC边上;③当点P在CD边上时.
(1)过点P作PE⊥CD于E.则根据题意,得:
EQ=16﹣2×3﹣2×2=6(cm),PE=AD=6cm;
在Rt△PEQ中,根据勾股定理,得:PE2+EQ2=PQ2,即36+36=PQ2,∴PQ=6![]() cm;
cm;
∴经过2s时P、Q两点之间的距离是6![]() cm;
cm;
(2)设x秒后,点P和点Q的距离是10cm.
(16﹣2x﹣3x)2+62=102,即(16﹣5x)2=64,∴16﹣5x=±8,∴x1=![]() ,x2=
,x2=![]() ;
;
∴经过![]() s或
s或![]() sP、Q两点之间的距离是10cm;
sP、Q两点之间的距离是10cm;
(3)连接BQ.设经过ys后△PBQ的面积为12cm2.
①当0≤y≤![]() 时,则PB=16﹣3y,∴
时,则PB=16﹣3y,∴![]() PBBC=12,即
PBBC=12,即![]() ×(16﹣3y)×6=12,解得:y=4;
×(16﹣3y)×6=12,解得:y=4;
②当![]() <y≤
<y≤![]() 时,BP=3y﹣AB=3y﹣16,QC=2y,则
时,BP=3y﹣AB=3y﹣16,QC=2y,则
![]() BPCQ=
BPCQ=![]() (3y﹣16)×2y=12,解得:y1=6,y2=﹣
(3y﹣16)×2y=12,解得:y1=6,y2=﹣![]() (舍去);
(舍去);
③![]() <y≤8时,QP=CQ﹣PC=2y﹣(3y﹣22)=22﹣y,则
<y≤8时,QP=CQ﹣PC=2y﹣(3y﹣22)=22﹣y,则
![]() QPCB=
QPCB=![]() (22﹣y)×6=12,解得:y=18(舍去).
(22﹣y)×6=12,解得:y=18(舍去).
综上所述:经过4秒或6秒△PBQ的面积为 12cm2.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
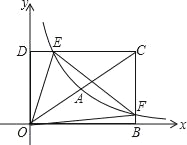
【题目】如图,在平面直角坐标系中,矩形DOBC的顶点O与坐标原点重合,B、D分别在坐标轴上,点C的坐标为(6,4),反比例函数y=![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.
(1)求反比例函数的解析式;
(2)求△OEF的面积;
(3)设直线EF的解析式为y=k2x+b,请结合图象直接写出不等式k2x+b>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
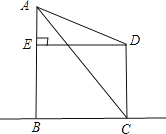
【题目】两建筑物AB和CD的水平距离为30米,如图所示,从A点测得太阳落山时,太阳光线AC照射到AB后的影子恰好在CD的墙角时的角度∠ACB=60°,又过一会儿,当AB的影子正好到达CD的楼顶D时的角度∠ADE=30°,DE⊥AB于E,则建筑物CD的高是多少米?(![]() ≈1.732,结果保留两位有效数字)
≈1.732,结果保留两位有效数字)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列给定的三点能确定一个圆的是( )
A. 线段![]() 的中点
的中点![]() 及两个端点
及两个端点
B. 角的顶点及角的边上的两点
C. 三角形的三个顶点
D. 矩形的对角线交点及两个顶点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两个圆,![]() 的半径等于篮球的半径,
的半径等于篮球的半径,![]() 的半径等于一个乒乓球的半径,现将两个圆的周长都增加
的半径等于一个乒乓球的半径,现将两个圆的周长都增加![]() 米,则面积增加较多的圆是( )
米,则面积增加较多的圆是( )
A. ![]() B.
B. ![]()
C. 两圆增加的面积是相同的 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
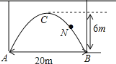
【题目】一拱形隧道的轮廓是抛物线如图,拱高![]() ,跨度
,跨度![]() .
.
![]() 建立适当的直角坐标系,求拱形隧道的抛物线关系式;
建立适当的直角坐标系,求拱形隧道的抛物线关系式;
![]() 拱形隧道下地平面是双向行车道(正中间是一条宽
拱形隧道下地平面是双向行车道(正中间是一条宽![]() 的隔离带),其中的一条行车道能否并排行驶宽
的隔离带),其中的一条行车道能否并排行驶宽![]() ,高
,高![]() 的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.
的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
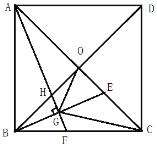
【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(不与O、C重合),作AF⊥BE,垂足为G,分别交BC、OB于F、H,连接OG、CG.
(1)求证:AH=BE;
(2)∠AGO的度数是否为定值?说明理由;
(3)若∠OGC=90°,BG=![]() ,求△OGC的面积.
,求△OGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
(1)求证:四边形AECD是菱形;
(2)若AB=6,BC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
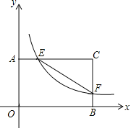
【题目】如图,四边形![]() 是矩形,
是矩形,![]() 为原点,
为原点,![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,![]() 是边
是边![]() 上的一个动点(不与
上的一个动点(不与![]() ,
,![]() 重合),过
重合),过![]() 点的反比例函数
点的反比例函数![]() 的图象与
的图象与![]() 边交于点
边交于点![]() .
.
![]() 当
当![]() 时,写出点
时,写出点![]() 、
、![]() 的坐标;
的坐标;
![]() 求
求![]() 的值;
的值;
![]() 是否存在这样的点
是否存在这样的点![]() ,使得将
,使得将![]() 沿
沿![]() 对折后,
对折后,![]() 点恰好落在
点恰好落在![]() 上?若存在,求出此时点
上?若存在,求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com