
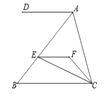
【题目】如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
(1)求证:四边形AECD是菱形;
(2)若AB=6,BC=10,求EF的长.

【答案】(1)证明见解析;(2) EF=![]() .
.
【解析】
(1)根据平行四边形和菱形的判定证明即可;
(2)根据菱形的性质和三角形的面积公式解答即可.
(1)证明:∵AD∥BC,AE∥DC,
∴四边形AECD是平行四边形.
∵在Rt△ABC中,∠BAC=90°,E是BC的中点,
∴BE=EC=AE.
∴四边形AECD是菱形.
(2)解:如图,过点A作AH⊥BC于点H.
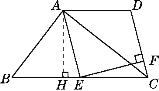
在Rt△ABC中,∠BAC=90°,AB=6,BC=10,由勾股定理得AC=8.
再根据面积关系,有S△ABC=![]() BC·AH=
BC·AH=![]() AB·AC,
AB·AC,
∴AH=![]() .
.
∵点E是BC的中点,BC=10,四边形AECD是菱形,
∴CD=CE=5.
∵S菱形AECD=CD·EF=CE·AH,
∴EF=AH=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.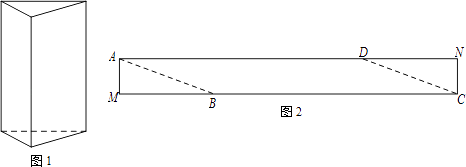
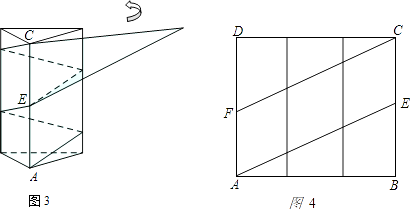
(1)请在图4中画出拼接后符合条件的平行四边形;
(2)请在图2中,计算裁剪的角度(即∠ABM的度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课外小组为了解同学们对学校“阳光跑操”活动的喜欢程度,抽取部分学生进行调查.被调查的每个学生按A(非常喜欢)、B(比较喜欢)、C(一般)、D(不喜欢)四个等级对活动评价.图(1)和图(2)是该小组采集数据后绘制的两幅统计图.经确认扇形统计图是正确的,而条形统计图尚有一处错误且并不完整.请你根据统计图提供的信息,解答下列问题:
(1)此次调查的学生人数为;
(2)条形统计图中存在错误的是(填A,B,C中的一个),并在图中加以改正;
(3)在图(2)中补画条形统计图中不完整的部分;
(4)如果该校有600名学生,那么对此活动“非常喜欢”和“比较喜欢”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下叙述正确的有( )
①对顶角相等;②同位角相等;③两直角相等;④邻补角相等;⑤多边形的外角和都相等;⑥三角形的中线把原三角形分成面积相等的两个三角形
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△;④CG⊥AE( )

A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
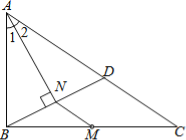
(1)求证:BN=DN;
(2)求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠DAC+∠ACB=180°,EF//BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°,则∠FEC的度数是( )
A.10°B.20°C.15°D.30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com