
ЎҫМвДҝЎҝИзНј1КЗТ»ёцИэАвЦщ°ьЧ°әРЈ¬ЛьөДөЧГжКЗұЯіӨОӘ10cmөДХэИэҪЗРОЈ¬ИэёцІаГж¶јКЗҫШРОЈ®ПЦҪ«ҝнОӘ15cmөДІКЙ«ҫШРОЦҪҙшAMCNІГјфіЙТ»ёцЖҪРРЛДұЯРОABCDЈЁИзНј2Ј©Ј¬И»әуУГХвМхЖҪРРЛДұЯРОЦҪҙш°ҙИзНј3өД·ҪКҪ°СХвёцИэАвЦщ°ьЧ°әРөДІаГжҪшРР°ьМщЈЁТӘЗу°ьМщКұГ»УРЦШөюІҝ·ЦЈ©Ј¬ЦҪҙшФЪІаГжІшИЖИэИҰЈ¬ХэәГҪ«ХвёцИэАвЦщ°ьЧ°әРөДІаГжИ«Іҝ°ьМщВъЈ®ФЪНј3ЦРЈ¬Ҫ«ИэАвЦщСШ№эөгAөДІаАвјфҝӘЈ¬өГөҪИзНј4өДІаГжХ№ҝӘНјЈ®ОӘБЛөГөҪІГјфөДҪЗ¶ИЈ¬ОТГЗҝЙТФёщҫЭХ№ҝӘНјЖҙҪУіц·ыәПМхјюөДЖҪРРЛДұЯРОҪшРРСРҫҝЈ®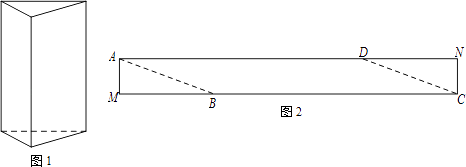
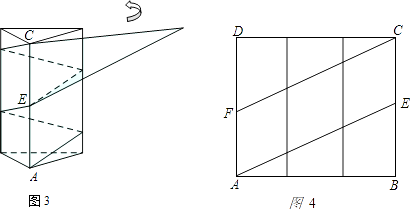
ЈЁ1Ј©ЗлФЪНј4ЦР»ӯіцЖҙҪУәу·ыәПМхјюөДЖҪРРЛДұЯРОЈ»
ЈЁ2Ј©ЗлФЪНј2ЦРЈ¬јЖЛгІГјфөДҪЗ¶ИЈЁјҙЎПABMөД¶ИКэЈ©Ј®
Ўҫҙр°ёЎҝ
ЈЁ1Ј©ҪвЈәИзНјЛщКҫЈә
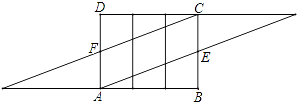
ЈЁ2Ј©ҪвЈәУЙНј2өД°ьМщ·Ҫ·ЁЦӘЈәABөДіӨөИУЪИэАвЦщөДөЧұЯЦЬіӨЈ¬
ЎаAB=30Ј®
ЎЯЦҪҙшҝнОӘ15Ј¬
ЎаsinЎПABM= ![]() Ј¬
Ј¬
ЎаЎПABM=30ЎгЈ®
ЎҫҪвОцЎҝЈЁ1Ј©КЧПИҪ«Нј4ЦРөДЎчABEПтЧуЖҪТЖ30cmЈ¬И»әуФЩҪ«ЎчCDFПтУТЖҪТЖ30cmјҙҝЙЈ»
ЈЁ2Ј©ёщҫЭABөДіӨөИУЪИэАвЦщөДөЧұЯЦЬіӨҝЙЗуөГAB=30cmЈ¬УЙЦҪҙшөДҝнОӘ15cmЈ¬ЧоәуЈ¬ТАҫЭМШКвИсҪЗИэҪЗәҜКэЦөҝЙЗуөГЎПAMB=30Ўг.
Ўҫҝјөгҫ«ОцЎҝҪвҙрҙЛМвөД№ШјьФЪУЪАнҪвјёәОМеөДХ№ҝӘНјөДПа№ШЦӘК¶Ј¬ХЖОХСШ¶аГжМеөДАвҪ«¶аГжМејфҝӘіЙЖҪГжНјРОЈ¬ИфёЙёцЖҪГжНјРОТІҝЙТФО§іЙТ»ёц¶аГжМеЈ»Н¬Т»ёц¶аГжМеСШІ»Н¬өДАвјфҝӘЈ¬өГөҪөДЖҪГжХ№ҝӘНјКЗІ»Т»СщөДЈ¬ҫНКЗЛөЈәН¬Т»ёцБўМеНјРОҝЙТФУР¶аЦЦІ»Н¬өДХ№ҝӘНјЈ¬ТФј°¶ФЖҪРРЛДұЯРОөДРФЦКөДАнҪвЈ¬БЛҪвЖҪРРЛДұЯРОөД¶ФұЯПаөИЗТЖҪРРЈ»ЖҪРРЛДұЯРОөД¶ФҪЗПаөИЈ¬БЪҪЗ»ҘІ№Ј»ЖҪРРЛДұЯРОөД¶ФҪЗПЯ»ҘПаЖҪ·ЦЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ№ШУЪxөДТ»ФӘ¶юҙО·ҪіМx2©Ғ3x©Ғk=0УРБҪёцІ»ПаөИөДКөКэёщЈ®
ЈЁ1Ј©ЗуkөДИЎЦө·¶О§Ј»
ЈЁ2Ј©ИфХвёц·ҪіМУРТ»ёцёщОӘ©Ғ2Ј¬ЗуkөДЦөәН·ҪіМөДБнТ»ёцёщЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝАЦАЦәНКэѧСЧйөДН¬С§ГЗСРҫҝБЛИзПВОКМвЈ¬ЗлДгТІАҙКФТ»ПВ°Й.
өг![]() КЗЦұПЯ
КЗЦұПЯ![]() ЙПТ»өгЈ¬ФЪН¬Т»ЖҪГжДЪЈ¬АЦАЦЛыГЗ°СТ»ёцөИСьЦұҪЗИэҪЗ°е
ЙПТ»өгЈ¬ФЪН¬Т»ЖҪГжДЪЈ¬АЦАЦЛыГЗ°СТ»ёцөИСьЦұҪЗИэҪЗ°е![]() ИОТв·ЕЈ¬ЖдЦРЦұҪЗ¶Ҙөг
ИОТв·ЕЈ¬ЖдЦРЦұҪЗ¶Ҙөг![]() Улөг
Улөг![]() ЦШәПЈ¬№эөг
ЦШәПЈ¬№эөг![]() ЧчЦұПЯ
ЧчЦұПЯ![]() Ј¬ҙ№ЧгОӘөг
Ј¬ҙ№ЧгОӘөг![]() Ј¬ҙУ№эөг
Ј¬ҙУ№эөг![]() Чч
Чч![]() Ј¬ҙ№ЧгОӘөг
Ј¬ҙ№ЧгОӘөг![]() .
.
ЈЁ1Ј©өұЦұПЯ![]() Ј¬
Ј¬![]() О»УЪөг
О»УЪөг![]() өДТмІаКұЈ¬ИзНј1Ј¬ПЯ¶О
өДТмІаКұЈ¬ИзНј1Ј¬ПЯ¶О![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ц®јдөДКэБҝ№ШПө___ЈЁІ»ұШЛөГчАнУЙЈ©Ј»
Ц®јдөДКэБҝ№ШПө___ЈЁІ»ұШЛөГчАнУЙЈ©Ј»
ЈЁ2Ј©өұЦұПЯ![]() Ј¬
Ј¬![]() О»УЪөг
О»УЪөг![]() өДУТІаКұЈ¬ИзНј2Ј¬ЕР¶ППЯ¶О
өДУТІаКұЈ¬ИзНј2Ј¬ЕР¶ППЯ¶О![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ц®јдөДКэБҝПөЈ¬ІўЛөГчАнУЙЈ»
Ц®јдөДКэБҝПөЈ¬ІўЛөГчАнУЙЈ»
ЈЁ3Ј©өұЦұПЯ![]() Ј¬
Ј¬![]() О»УЪөг
О»УЪөг![]() өДЧуІаКұЈ¬ИзНј3Ј¬ЗлДгІ№И«НјРОЈ¬ІўЦұҪУРҙіцПЯ¶О
өДЧуІаКұЈ¬ИзНј3Ј¬ЗлДгІ№И«НјРОЈ¬ІўЦұҪУРҙіцПЯ¶О![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ц®јдөДКэБҝ№ШПө.
Ц®јдөДКэБҝ№ШПө.



Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
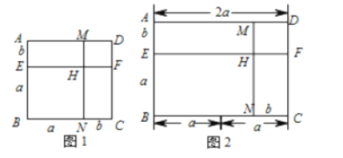
ЎҫМвДҝЎҝЈЁ1Ј©ОТГЗТСҫӯЦӘөАЈ¬ёщҫЭјёәОНјРОөДГж»э№ШПөҝЙТФЛөГчНкИ«ЖҪ·Ҫ№«КҪЈ¬ЛөГчИзПВЈәИзНј1Ј®Хэ·ҪРО![]() өДГж»э=Хэ·ҪРО
өДГж»э=Хэ·ҪРО![]() өДГж»э+ЈЁіӨ·ҪРО
өДГж»э+ЈЁіӨ·ҪРО![]() +іӨ·ҪРО
+іӨ·ҪРО![]() өДГж»эЈ©+Хэ·ҪРО
өДГж»эЈ©+Хэ·ҪРО![]() өДГж»эЈ®јҙЈә
өДГж»эЈ®јҙЈә![]() Ј®
Ј®
ЈЁ2Ј©»№УРТ»Р©өИКҪТІҝЙТФУГЙПКц·ҪКҪјУТФЛөГчЈ¬ЗлДгіўКФНкіЙЈ®ИзНј2Ј¬іӨ·ҪРО![]() өДГж»э=іӨ·ҪРО
өДГж»э=іӨ·ҪРО![]() өДГж»э+іӨ·ҪРО
өДГж»э+іӨ·ҪРО![]() өДГж»э-іӨ·ҪРО
өДГж»э-іӨ·ҪРО![]() өДГж»э-________өДГж»эЈ¬јҙ
өДГж»э-________өДГж»эЈ¬јҙ![]() ________________Ј®
________________Ј®
ЈЁ3Ј©јЖЛг![]() =______________Ј®ТАХХЙПКц·Ҫ·ЁЈ¬»ӯНјІўЛөГчЈ®
=______________Ј®ТАХХЙПКц·Ҫ·ЁЈ¬»ӯНјІўЛөГчЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДі¶ОМъВ·БҪЕФ°ІЦГБЛБҪЧщҝЙРэЧӘМҪХХөЖЈ¬ЦчөАВ·КЗЖҪРРЈ¬јҙPQЎОMNЈ® ИзНјЛщКҫЈ¬өЖAЙдПЯҙУAMҝӘКјЛіКұХлРэЧӘЦБANұгБўјҙ»ШЧӘЈ¬өЖBЙдПЯҙУBPҝӘКјЛіКұХлРэЧӘЦБBQұгБўјҙ»ШЧӘЈ¬БҪөЖІ»НЈҪ»ІжХХЙдСІКУЈ®ИфөЖAЧӘ¶ҜөДЛЩ¶ИКЗГҝГл2¶ИЈ¬өЖBЧӘ¶ҜөДЛЩ¶ИКЗГҝГл1¶ИЈ® ИфөЖBЙдПЯПИЧӘ¶Ҝ30ГлЈ¬өЖAЙдПЯІЕҝӘКјЧӘ¶ҜЈ¬ФЪөЖBЙдПЯөҪҙпBQЦ®З°Ј¬AөЖЧӘ¶Ҝ_________ГлЈ¬БҪөЖөД№вКш»ҘПаЖҪРРЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬Хэ·ҪРОABCDұЯіӨОӘ4Ј¬өгPҙУөгAФЛ¶ҜөҪөгBЈ¬ЛЩ¶ИОӘ1Ј¬өгQСШB©ҒC©ҒDФЛ¶ҜЈ¬ЛЩ¶ИОӘ2Ј¬өгPЎўQН¬Кұіц·ўЈ¬ФтЎчBPQөДГж»эyУлФЛ¶ҜКұјдtЈЁtЎЬ4Ј©өДәҜКэНјПуКЗЈЁ Ј©
A.
B.
C.
D.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘКэЦбЙПөг![]() ұнКҫөДКэОӘ8Ј¬
ұнКҫөДКэОӘ8Ј¬![]() КЗКэЦбЙПО»УЪөг
КЗКэЦбЙПО»УЪөг![]() ЧуІаТ»өгЈ¬ЗТ
ЧуІаТ»өгЈ¬ЗТ![]() Ј¬¶Ҝөг
Ј¬¶Ҝөг![]() ҙУ
ҙУ![]() өгіц·ўЈ¬ТФГҝГл5ёцөҘО»іӨ¶ИөДЛЩ¶ИСШКэЦбПтЧуФИЛЩФЛ¶ҜЈ¬ЙиФЛ¶ҜКұјдОӘ
өгіц·ўЈ¬ТФГҝГл5ёцөҘО»іӨ¶ИөДЛЩ¶ИСШКэЦбПтЧуФИЛЩФЛ¶ҜЈ¬ЙиФЛ¶ҜКұјдОӘ![]() ГлЈ®
ГлЈ®
ЈЁ1Ј©КэЦбЙПөг![]() ұнКҫөДКэКЗ___________Ј»өг
ұнКҫөДКэКЗ___________Ј»өг![]() ұнКҫөДКэКЗ___________(УГә¬
ұнКҫөДКэКЗ___________(УГә¬![]() өДҙъКэКҪұнКҫ)
өДҙъКэКҪұнКҫ)
ЈЁ2Ј©¶Ҝөг![]() ҙУөг
ҙУөг![]() іц·ўЈ¬ТФГҝГл3ёцөҘО»іӨ¶ИөДЛЩ¶ИСШКэЦбПтУТФИЛЩФЛ¶ҜЈ¬Ифөг
іц·ўЈ¬ТФГҝГл3ёцөҘО»іӨ¶ИөДЛЩ¶ИСШКэЦбПтУТФИЛЩФЛ¶ҜЈ¬Ифөг![]() Н¬Кұіц·ўЈ¬ОК¶аЙЩГлКұ
Н¬Кұіц·ўЈ¬ОК¶аЙЩГлКұ![]() Ц®јдөДҫаАлЗЎәГөИУЪ2Јҝ
Ц®јдөДҫаАлЗЎәГөИУЪ2Јҝ
ЈЁ3Ј©Иф![]() ОӘ
ОӘ![]() өДЦРөгЈ¬
өДЦРөгЈ¬![]() ОӘ
ОӘ![]() өДЦРөгЈ¬ФЪөг
өДЦРөгЈ¬ФЪөг![]() ФЛ¶ҜөД№эіМЦРЈ¬ПЯ¶О
ФЛ¶ҜөД№эіМЦРЈ¬ПЯ¶О![]() өДіӨ¶ИКЗ·с·ўЙъұд»ҜЈҝИфұд»ҜЈ¬ЗлЛөГчАнУЙЈ¬ИфІ»ұдЈ¬ЗлДг»ӯіцНјРОЈ¬ІўЗуіцПЯ¶О
өДіӨ¶ИКЗ·с·ўЙъұд»ҜЈҝИфұд»ҜЈ¬ЗлЛөГчАнУЙЈ¬ИфІ»ұдЈ¬ЗлДг»ӯіцНјРОЈ¬ІўЗуіцПЯ¶О![]() өДіӨЈ®
өДіӨЈ®
![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЕЧОпПЯy=ax2+bx+cөД¶ФіЖЦбКЗx=©Ғ1Ј®ЗТ№эөгЈЁ ![]() Ј¬0Ј©Ј¬УРПВБРҪбВЫЈәўЩabcЈҫ0Ј»
Ј¬0Ј©Ј¬УРПВБРҪбВЫЈәўЩabcЈҫ0Ј»
ўЪa©Ғ2b+4c=0Ј» ўЫ25a©Ғ10b+4c=0Ј» ўЬ3b+2cЈҫ0Ј» ўЭa©ҒbЎЭmЈЁam©ҒbЈ©Ј»
ЖдЦРЛщУРХэИ·өДҪбВЫКЗЈЁ Ј©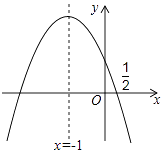
A.ўЩўЪўЫ
B.ўЩўЫўЬ
C.ўЩўЪўЫўЭ
D.ўЩўЫўЭ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЛДұЯРОABCDЦРЈ¬ЎПBACЈҪ90ЎгЈ¬EКЗBCөДЦРөгЈ¬ADЎОBCЈ¬AEЎОDCЈ¬EFЎНCDУЪөгF.
(1)ЗуЦӨЈәЛДұЯРОAECDКЗБвРОЈ»
(2)ИфABЈҪ6Ј¬BCЈҪ10Ј¬ЗуEFөДіӨЈ®

Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com