
【题目】关于x的一元二次方程x2﹣3x﹣k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若这个方程有一个根为﹣2,求k的值和方程的另一个根.
【答案】
(1)解:∵关于x的一元二次方程x2﹣3x﹣k=0有两个不相等的实数根,
∴△>0,
∴9+4k>0,
∴k>﹣ ![]() ,
,
∴k的取值范围k>﹣ ![]()
(2)解:把x=﹣2代入x2﹣3x﹣k=0得k=10,
∴方程x2﹣3x﹣10=0的两根为x1=﹣2,x2=5,
综上所述,k=10,x2=5.
【解析】(1)根据根与系数的关系得出k的取值范围;(2)把x=﹣2代入方程得出k的值,再解方程即可.
【考点精析】本题主要考查了求根公式和根与系数的关系的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.
【1】如图1,若点P在BC边上,此时PD=0,易证PD,PE,PF与AB满足的数量关系PD+PE+PF=AB;当点P在△ABC内,先在图2中作出图形,并写出PD,PE,PF与AB满足的数量关系,然后证明你的结论
【2】当点P在△ABC外,先在图3中作出图形,然后写出PD,PE,PF与AB满足的数量关系.(不用说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空:
①画出图中△ABC的高AD(标注出点D的位置);
②画出把△ABC沿射线AD方向平移2cm后得到的△A1B1C1;
③根据“图形平移”的性质,得BB1=_____cm,AC与A1C1的位置关系是_____,数量关系是:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
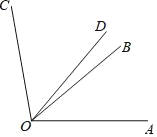
【题目】补全解题过程.
已知:如图,∠AOB=40°,∠BOC=60°,OD平分∠AOC.求∠BOD的度数.
解:∵∠AOC=∠AOB+∠ ,
又∵∠AOB=40°,∠BOC=60°,
∴∠AOC= °.
∵OD平分∠AOC,
∴∠AOD= ∠AOC( ).
∴∠AOD=50°.
∴∠BOD=∠AOD﹣∠ .
∴∠BOD= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地,甲出发0.5h后乙开始出发,结果比甲早1(h)到达B地,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,a表示A、B两地之间的距离.请结合图中的信息解决如下问题: 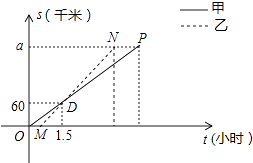
(1)分别计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回,请问甲车到达B地后以多大的速度立即匀速返回,才能与乙车同时回到A地?并在图中画出甲、乙两车在返回过程中离A地的距离S(km)与时间t(h)的函数图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
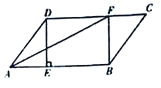
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.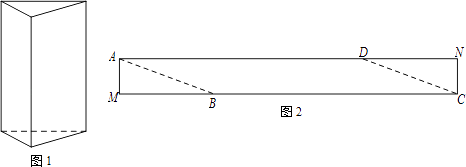
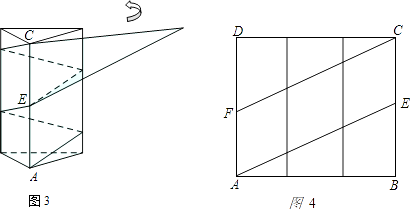
(1)请在图4中画出拼接后符合条件的平行四边形;
(2)请在图2中,计算裁剪的角度(即∠ABM的度数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com