
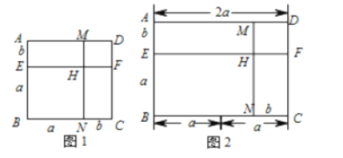
【题目】(1)我们已经知道,根据几何图形的面积关系可以说明完全平方公式,说明如下:如图1.正方形![]() 的面积=正方形
的面积=正方形![]() 的面积+(长方形
的面积+(长方形![]() +长方形
+长方形![]() 的面积)+正方形
的面积)+正方形![]() 的面积.即:
的面积.即:![]() .
.
(2)还有一些等式也可以用上述方式加以说明,请你尝试完成.如图2,长方形![]() 的面积=长方形
的面积=长方形![]() 的面积+长方形
的面积+长方形![]() 的面积-长方形
的面积-长方形![]() 的面积-________的面积,即
的面积-________的面积,即![]() ________________.
________________.
(3)计算![]() =______________.依照上述方法,画图并说明.
=______________.依照上述方法,画图并说明.
【答案】(2)正方形MHFD,2a2+ab﹣b2;(3)2a2+3ab+b2.
【解析】
(2)利用长方形ABNM的面积=长方形EBCF的面积+长方形AEFD的面积﹣长方形HNCF的面积﹣正方形MHFD的面积计算.
(3)利用长方形ABCD的面积=正方形GBHF的面积+正方形FHQN的面积+长方形AGFE的面积+长方形EFNM的面积+长方形NQCO的面积+正方形MNOD的面积计算.
解:(2)长方形ABNM的面积=长方形EBCF的面积+长方形AEFD的面积﹣长方形HNCF的面积﹣正方形MHFD的面积,即:(2a﹣b)(a+b)=2a2+ab﹣b2.
故答案为:正方形MHFD,2a2+ab﹣b2.
(3)(2a+b)(a+b)=2a2+3ab+b2.
如图,

∵长方形ABCD的面积=正方形GBHF的面积+正方形FHQN的面积+长方形AGFE的面积+长方形EFNM的面积+长方形NQCO的面积+正方形MNOD的面积
∴(2a+b)(a+b)= a2+ a2+ ab+ ab+ ab+ b2=2a2+3ab+b2
故答案为:2a2+3ab+b2.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】补全解题过程.
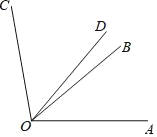
已知:如图,∠AOB=40°,∠BOC=60°,OD平分∠AOC.求∠BOD的度数.
解:∵∠AOC=∠AOB+∠ ,
又∵∠AOB=40°,∠BOC=60°,
∴∠AOC= °.
∵OD平分∠AOC,
∴∠AOD= ∠AOC( ).
∴∠AOD=50°.
∴∠BOD=∠AOD﹣∠ .
∴∠BOD= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用网格画图:
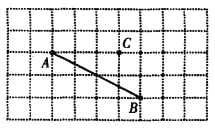
(1)过点C画AB的平行线CD;
(2)过点C画AB的垂线,垂足为E;
(3)线段CE的长度是点C到直线_______的距离;
(4)连接CA、CB,在线段CA、CB、CE中,线段_______最短,理由:_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步了解八年级学生的身体素质情况,体育老师对八年级(1)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出不完整的频数分布表和频数分布直方图(如图).
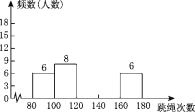
组别 | 次数(x) | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)表中的a=________;
(2)请把频数分布直方图补充完整;
(3)若规定:x<120为不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.根据以上信息,请你给学校或八年级同学提一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1 , x2 , 其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b<0,b2+8a>4ac,a<﹣1,其中结论正确的有( )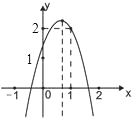
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.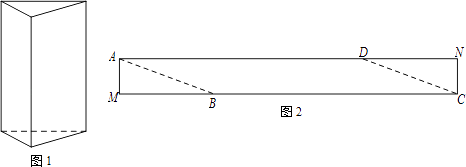
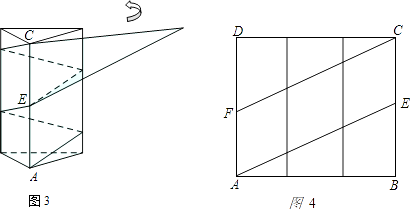
(1)请在图4中画出拼接后符合条件的平行四边形;
(2)请在图2中,计算裁剪的角度(即∠ABM的度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高铁的开通,给衢州市民出行带来了极大的方便,“五一”期间,乐乐和颖颖相约到杭州市的某游乐园游玩,乐乐乘私家车从衢州出发1小时后,颖颖乘坐高铁从衢州出发,先到杭州火车站,然后再转车出租车取游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(千米)与乘车时间t(小时)的关系如图所示.
请结合图象解决下面问题:

(1)高铁的平均速度是每小时多少千米?
(2)当颖颖达到杭州火车东站时,乐乐距离游乐园还有多少千米?
(3)若乐乐要提前18分钟到达游乐园,问私家车的速度必须达到多少千米/小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com