
【题目】如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△;④CG⊥AE( )

A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
【答案】B
【解析】根据题意,结合图形,对选项一一求证,判定正确选项
解:在□ABCD中,∠ADC=∠ABC,AD=BC,CD=AB,
∵△ABE、△ADF都是等边三角形,
∴AD=DF,AB=EB,∠ADF=∠ABE=60°,
∴DF=BC,CD=BC,
∴∠CDF=360°-∠ADC-60°=300°-∠ADC,
∠EBC=360°-∠ABC-60°=300°-∠ABC,
∴∠CDF=∠EBC,
在△CDF和△EBC中,
DF=BC,∠CDF=∠EBC,CD=EB,
∴△CDF≌△EBC(SAS),故①正确;
在ABCD中,∠DAB=180°-∠ADC,
∴∠EAF=∠DAB+∠DAF+∠BAE=180°-∠ADC+60°+60°=300°-∠ADC,
∴∠CDF=∠EAF,故②正确;
同理可证△CDF≌△EAF,
∴EF=CF,
∵△CDF≌△EBC,
∴CE=CF,
∴EC=CF=EF,
∴△ECF是等边三角形,故③正确;
当CG⊥AE时,∵△ABE是等边三角形,
∴∠ABG=30°,
∴∠ABC=180°-30°=150°,
∵∠ABC=150°无法求出,故④错误;
综上所述,正确的结论有①②③.
故选B.
“点睛”本题考查了全等三角形的判定、等边三角形的判定和性质、平行线的性质等知识,综合性强,考查学生综合运用数学知识的能力.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点E处,若∠EBC=20°,则∠EBD的度数为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图4所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为_________________________________.
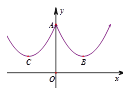
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小聪遇到这样一个有关角平分线的问题:如图1,在△ABC中,∠A=2∠B,CD平分∠ACB,AD=2.2,AC=3.6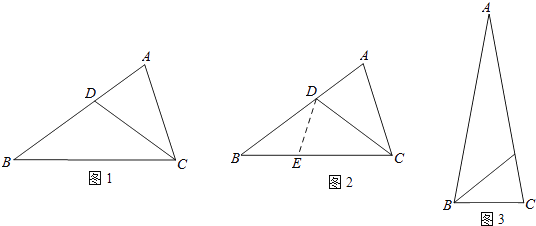
求BC的长.
小聪思考:因为CD平分∠ACB,所以可在BC边上取点E,使EC=AC,连接DE.这样很容易得到△DEC≌△DAC,经过推理能使问题得到解决(如图2).
请回答:
(1)△BDE是三角形.
(2)BC的长为 .
参考小聪思考问题的方法,解决问题:
如图3,已知△ABC中,AB=AC,∠A=20°,BD平分∠ABC,BD=2.3,BC=2.求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com