
【题目】一次函数y=ax+b(a≠0)的图象与反比例函数y= ![]() (k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(﹣1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.
(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(﹣1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.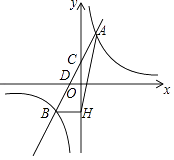
(1)求一次函数和反比例函数的解析式;
(2)求△ABH面积.
【答案】
(1)解:∵点D的坐标为(﹣1,0),tan∠CDO=2,
∴CO=2,即C(0,2),
把C(0,2),D(﹣1,0)代入y=ax+b可得,
![]() ,解得
,解得 ![]() ,
,
∴一次函数解析式为y=2x+2,
∵点A的横坐标是1,
∴当x=1时,y=4,即A(1,4),
把A(1,4)代入反比例函数y= ![]() ,可得k=4,
,可得k=4,
∴反比例函数解析式为y= ![]()
(2)解:解方程组 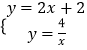 ,可得
,可得 ![]() 或
或 ![]() ,
,
∴B(﹣2,﹣2),
又∵A(1,4),BH⊥y轴,
∴△ABH面积= ![]() ×2×(4+2)=6.
×2×(4+2)=6.
【解析】(1)先由tan∠CDO=2可求出C坐标,再把D点坐标代入直线解析式,可求出一次函数解析式,再由直线解析式求出A坐标,代入双曲线解析式,可求出双曲线解析式;(2)△ABH面积可以BH为底,高=yA-yB=4-(-2)=6.
【考点精析】根据题目的已知条件,利用解直角三角形的相关知识可以得到问题的答案,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )

A. 120° B. 125° C. 135° D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知一个多边形的内角和是它的外角和的 3 倍,求这个多边形的边数.
(2)如图,点F 是△ABC 的边 BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1).
(1)继续填写:A6(________,________),A7(________,________),A8(________,________),A9((________,________).A10((________,________),A11(________,________),A12(________,________),A13(________,________).
(2)写出点A2010(________,________),A2011(________,________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,
,![]() ,
,![]() ,把
,把![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度逆时针方向旋转一周,同时
的速度逆时针方向旋转一周,同时![]() 绕
绕![]() 点以每秒
点以每秒![]() 的速度逆时针方向旋转,当
的速度逆时针方向旋转,当![]() 停止旋转时
停止旋转时![]() 也随之停止旋转.设旋转后的两个角分别记为
也随之停止旋转.设旋转后的两个角分别记为![]() 、
、![]() ,旋转时间为
,旋转时间为![]() 秒.
秒.
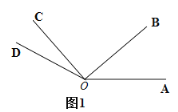
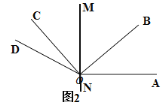
(1)如图2,直线![]() 垂直于
垂直于![]() ,将
,将![]() 沿直线
沿直线![]() 翻折至
翻折至![]() ,请你直接写出
,请你直接写出![]() 的度数,不必说明理由;
的度数,不必说明理由;
(2)如图1,在旋转过程中,若射线![]() 与
与![]() 重合时,求
重合时,求![]() 的值;
的值;
(3)如图1,在旋转过程中,当![]() 时,直接写出
时,直接写出![]() 的值,不必说明理由.
的值,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角坐标平面内两点A(-2,-3)、B(3,-3),将点B向上平移5个单位到达点C,求:

(1)A、B两点间的距离;
(2)写出点C的坐标;
(3)四边形OABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将△ABC平移到△A′B′C′的位置,连接BB′,AA′,CC′,平移的方向是点______到点________的方向,平移的距离是线段______的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC的∠C折起,翻折后角的顶点位置记作C′,当C′落在AC上时(如图1),易证:∠1=2∠2.
当C′点落在CA和CB之间(如图2)时,或当C′落在CB、CA的同旁(如图3)时,∠1、∠2、∠3关系又如何?请写出你的猜想,并就其中一种情况给出证明.



图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE、CF相交于点D,则①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的是( ) 
A.①
B.②
C.①②
D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com