
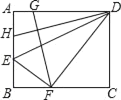
【题目】如图,将矩形ABCD沿DE折叠,点A恰好落在BC上的点F处,点G、H分别在AD、AB上,且FG⊥DH,若tan∠ADE=![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
利用翻折变换的性质得出△EBF∽△FCD,进而求出![]() 的值,再利用已知得出得△GNF∽△DAH,则
的值,再利用已知得出得△GNF∽△DAH,则![]() .
.
∵将矩形ABCD沿DE折叠,点A恰好落在BC上的点F处,
∴AE=EF,∠EFD=90°,
∴∠EFB+∠DFC=90°,
∵∠DFC+∠CDF=90°,
∴∠CDF=∠EFB,
又∵∠B=∠C,
∴△EBF∽△FCD,
∴![]() ,
,
∵tan∠ADE=![]() ,
,
∴tan∠EDF=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴设BE=a,BF=x,则FC=2a,DC=2x,
故EF+BE=DC,
则![]() +a=2x,
+a=2x,
整理得:a=![]() x,
x,
故![]() =
= =
=![]() ,
,
过点G作GN⊥BC于点N,
∴四边形ABNG是矩形,
∴AB=GN=DC,∠GNF=∠NGD=90°,
∴∠NGF+∠FGD=90°,
∵FG⊥DH,四边形ABCD是矩形,
∴AD=BC,∠FGD+∠GDM=90°,∠GNF=∠A,
∴∠GDM=∠NGF,
∴△GNF∽△DAH,
∴![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
故选:B.



科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 是坐标原点,直线
是坐标原点,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于
轴于![]() 、
、![]() 两点.
两点.

(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 为直线
为直线![]() 上一动点,以
上一动点,以![]() 为顶点的抛物线
为顶点的抛物线![]() 与直线
与直线![]() 的另一交点为
的另一交点为 ![]() (如图1),连
(如图1),连![]() 、
、![]() ,在点
,在点![]() 的运动过程中
的运动过程中![]() 的面积
的面积![]() 是否变化,若变化,求出
是否变化,若变化,求出![]() 的范围;若不变,求出
的范围;若不变,求出![]() 的值;
的值;
(3)平移(2)中的抛物线,使顶点为![]() ,抛物线与
,抛物线与![]() 轴的正半轴交于点
轴的正半轴交于点![]() (如图2) ,
(如图2) ,![]() ,
,![]() 为抛物线上两点,若以
为抛物线上两点,若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,求直线
,求直线![]() 经过的定点
经过的定点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
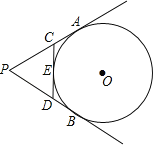
【题目】如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
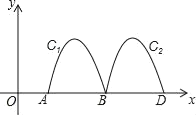
【题目】如图,抛物线y=﹣x2+4x﹣3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得到C2,C2与x轴交于B、D两点.若直线y=kx﹣k与C1、C2共有3个不同的交点,则k的最大值是( )
A.![]() B.2
B.2![]() ﹣6C.6+4
﹣6C.6+4![]() D.6﹣4
D.6﹣4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过坐标原点,与
经过坐标原点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,且顶点
,且顶点![]() 坐标为
坐标为![]() .
.
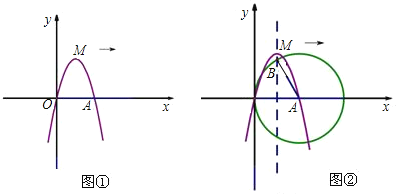
(1)求抛物线解析式.
(2)将抛物线向右平移![]() 个单位,所得抛物线与
个单位,所得抛物线与![]() 轴交于
轴交于![]() 两点,与原抛物线交于点
两点,与原抛物线交于点![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]()
![]() 的函数关系式.
的函数关系式.
(3)如图②,以点![]() 为圈心,以线段
为圈心,以线段![]() 为半径画圆,交抛物线
为半径画圆,交抛物线![]() 的对称轴于点
的对称轴于点![]() ,连结
,连结![]() ,若将抛物线向右平移
,若将抛物线向右平移![]() 个单位后,
个单位后,![]() 点的对应点为
点的对应点为![]() ,
,![]() 点的对应点为
点的对应点为![]() ,且满足四边形
,且满足四边形![]() 为菱形,平移后的抛物线的对称轴与菱形的对角线
为菱形,平移后的抛物线的对称轴与菱形的对角线![]() 交于点
交于点![]() 问:在
问:在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得以
,使得以![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出F点坐标,若不存在,请说明理由.
相似?若存在,求出F点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:直线y=x与反比例函数y=![]() (k>0)的图象在第一象限内交于点A(2,m).
(k>0)的图象在第一象限内交于点A(2,m).
(1)求m、k的值;
(2)点B在y轴负半轴上,若△AOB的面积为2,求AB所在直线的函数表达式;
(3)将△AOB沿直线AB向上平移,平移后A、O、B的对应点分别为A'、O'、B',当点O'恰好落在反比例函数y=![]() 的图象上时,求点A'的坐标.
的图象上时,求点A'的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
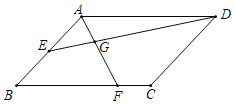
【题目】如图,平行四边形ABCD的边长AD=3,AB=2,∠BAD=120°,E为AB的中点,F在边BC上,且BF=2FC.AF与DE交于点G,则AG的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,某市发出“节能减排,绿色出行”的倡导,某企业抓住机遇投资20万元购买并投放一批A型“共享单车”,因为单车需求量增加,计划继续投放B型单车,B型单车的投放数量与A型单车的投放数量相同,投资总费用减少20%,购买B型单车的单价比购买A型单车的单价少50元,则A型单车每辆车的价格是多少元?设A型单车每辆车的价格为x元,根据题意,列方程正确的是( )
A.![]() =
=![]()
B.![]() =
=![]()
C.![]() =
=![]()
D.![]() =
=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给以下结论:①abc<0;②c+2a<0;③9a﹣3b+c=0;④a﹣b≥m(am+b)(m为实数);⑤4ac﹣b2<0.其中错误结论的个数有( )
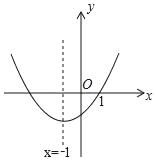
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com