
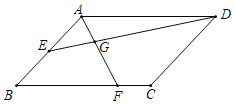
【题目】如图,平行四边形ABCD的边长AD=3,AB=2,∠BAD=120°,E为AB的中点,F在边BC上,且BF=2FC.AF与DE交于点G,则AG的长为_____.
【答案】![]()
【解析】
延长DE交直线BC于H,如图,利用平行四边形的性质和边长之间的关系证明△ABF为等边三角形得到AF=AB=2,再证明△ADE≌△BEH得到BH=AD=3,然后证明△ADG∽△FHG得到![]() =
=![]() =
=![]() ,最后利用比例性质计算出AG.
,最后利用比例性质计算出AG.
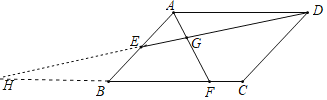
延长DE交直线BC于H,如图,
∵四边形ABCD为平行四边形,
∴BC=AD=3,AD∥BC,
∴∠B=180°﹣∠BAD=180°﹣120°=60°,
∵AD=3,AB=2,BF=2FC,
∴BF=2=AB,
∴△ABF为等边三角形,
∴AF=AB=2,
∵E为AB的中点,
∴AE=BE,
而∠H=∠ADE,∠AED=∠BEH,
∴△ADE≌△BEH,
∴BH=AD=3,
∵AD∥FH,
∴△ADG∽△FHG,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AG=![]() ×2=
×2=![]() .
.
故答案为![]() .
.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
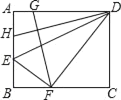
【题目】如图,将矩形ABCD沿DE折叠,点A恰好落在BC上的点F处,点G、H分别在AD、AB上,且FG⊥DH,若tan∠ADE=![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
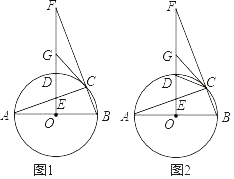
【题目】如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG
(1)判断CG与⊙O的位置关系,并说明理由;
(2)求证:2OB2=BCBF;
(3)如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店积极响应政府“改革创新,奋发有为”的号召,举办“读书节“系列活动.活动中故事类图书的标价是典籍类图书标价的1.5倍,若顾客用540元购买图书,能单独购买故事类图书的数量恰好比单独购买典籍类图书的数量少10本.
(1)求活动中典籍类图书的标价;
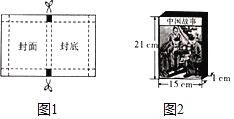
(2)该店经理为鼓励广大读者购书,免费为购买故事类的读者赠送图1所示的精致矩形包书纸.在图1的包书纸示意图中,虚线是折痕,阴影是裁剪掉的部分,四角均为大小相同的正方形,正方形的边长为折叠进去的宽度.已知该包书纸的面积为875cm2(含阴影部分),且正好可以包好图2中的《中国故事》这本书,该书的长为21cm,宽为15cm,厚为1cm,请直接写出该包书纸包这本书时折叠进去的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据函数学习中积累的知识与经验,李老师要求学生探究函数y=![]() +1的图象.同学们通过列表、描点、画图象,发现它的图象特征,请你补充完整.
+1的图象.同学们通过列表、描点、画图象,发现它的图象特征,请你补充完整.
(1)函数y=![]() +1的图象可以由我们熟悉的函数 的图象向上平移 个单位得到;
+1的图象可以由我们熟悉的函数 的图象向上平移 个单位得到;
(2)函数y=![]() +1的图象与x轴、y轴交点的情况是: ;
+1的图象与x轴、y轴交点的情况是: ;
(3)请你构造一个函数,使其图象与x轴的交点为(2,0),且与y轴无交点,这个函数表达式可以是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
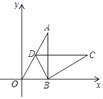
【题目】如图,直线![]() 经过点A,作AB⊥x轴于点B,将△ABO绕点B顺时针旋转60°得到△CBD,若点B的坐标为(1,0),则点C的坐标为( )
经过点A,作AB⊥x轴于点B,将△ABO绕点B顺时针旋转60°得到△CBD,若点B的坐标为(1,0),则点C的坐标为( )
A.(3,![]() )B.(
)B.(![]() ,
,![]() )C.(3,
)C.(3,![]() )D.(
)D.(![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com