
【题目】如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG
(1)判断CG与⊙O的位置关系,并说明理由;
(2)求证:2OB2=BCBF;
(3)如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.
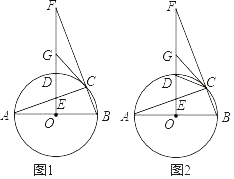
【答案】(1)CG与⊙O相切,理由见解析;(2)见解析;(3)DE=2
【解析】
(1)连接CE,由AB是直径知△ECF是直角三角形,结合G为EF中点知∠AEO=∠GEC=∠GCE,再由OA=OC知∠OCA=∠OAC,根据OF⊥AB可得∠OCA+∠GCE=90°,即OC⊥GC,据此即可得证;
(2)证△ABC∽△FBO得![]() ,结合AB=2BO即可得;
,结合AB=2BO即可得;
(3)证ECD∽△EGC得![]() ,根据CE=3,DG=2.5知
,根据CE=3,DG=2.5知![]() ,解之可得.
,解之可得.
解:(1)CG与⊙O相切,理由如下:
如图1,连接CE,
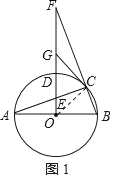
∵AB是⊙O的直径,
∴∠ACB=∠ACF=90°,
∵点G是EF的中点,
∴GF=GE=GC,
∴∠AEO=∠GEC=∠GCE,
∵OA=OC,
∴∠OCA=∠OAC,
∵OF⊥AB,
∴∠OAC+∠AEO=90°,
∴∠OCA+∠GCE=90°,即OC⊥GC,
∴CG与⊙O相切;
(2)∵∠AOE=∠FCE=90°,∠AEO=∠FEC,
∴∠OAE=∠F,
又∵∠B=∠B,
∴△ABC∽△FBO,
∴![]() ,即BOAB=BCBF,
,即BOAB=BCBF,
∵AB=2BO,
∴2OB2=BCBF;
(3)由(1)知GC=GE=GF,
∴∠F=∠GCF,
∴∠EGC=2∠F,
又∵∠DCE=2∠F,
∴∠EGC=∠DCE,
∵∠DEC=∠CEG,
∴△ECD∽△EGC,
∴![]() ,
,
∵CE=3,DG=2.5,
∴![]() ,
,
整理,得:DE2+2.5DE﹣9=0,
解得:DE=2或DE=﹣4.5(舍),
故DE=2.


科目:初中数学 来源: 题型:
【题目】某游乐场新推出了一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯AB自由上下选择项目难度.其中斜坡轨道BC的坡度(或坡比)为i=1:2,BC=12![]() 米,CD=8米,∠D=36°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.(精确到0.1米,参考数据:tan36°≈0.73,cos36°≈0.81,sin36°≈0.59)
米,CD=8米,∠D=36°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.(精确到0.1米,参考数据:tan36°≈0.73,cos36°≈0.81,sin36°≈0.59)
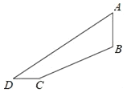
A.5.6B.6.9C.11.4D.13.9
查看答案和解析>>
科目:初中数学 来源: 题型:
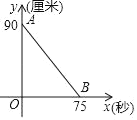
【题目】某工地需要利用炸药实施爆破,操作人员点燃导火线后,要在炸药爆炸前跑到300米以外的安全区域,炸药导火线的长度y(厘米)与燃烧的时间x(秒)之间的函数关系如图所示.
(1)请写出点B的实际意义,
(2)求y与x之间的函数关系式,并写出自变量的取值范围.
(3)问操作人员跑步的速度必须超过多少,才能保证安全.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
观察与思考:阅读下列材料,并解决后面的问题.在锐角![]() 中,
中,![]() 、
、![]() 、
、![]() 的对边分别是a、b、c,过A作
的对边分别是a、b、c,过A作![]() 于D(如图),则
于D(如图),则![]() ,
,![]() ,即
,即![]() ,
,![]() ,于是
,于是![]() ,即
,即![]() .同理有:
.同理有:![]() ,
,![]() ,所以
,所以![]() .
.
即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.
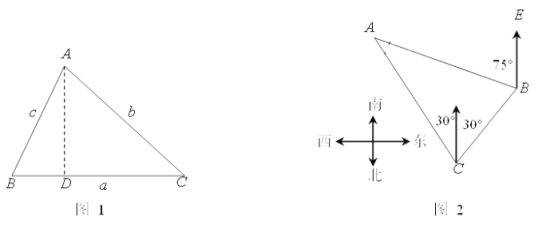
(1)如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
(2)如图,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A的距离AB.
(3)在(2)的条件下,试求75°的正弦值.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E为矩形ABCD的边AD上一点,点P从点B出发沿BE→ED→DC运动到点C停止,点Q从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.若点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t之间的函数图象如图2所示.给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②S△ABE=48cm2;③14<t<22时,y=110﹣5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤当△BPQ与△BEA相似时,t=14.5.其中正确结论的序号是( )

A. ①④⑤ B. ①②④ C. ①③④ D. ①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
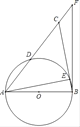
【题目】如图,在等腰△ABC中,AB=BC,以AB为直径的半圆分别交AC、BC于点D、E两点,BF与⊙O相切于点B,交AC的延长线于点F.
(1)求证:D是AC的中点;
(2)若AB=12,sin∠CAE=![]() ,求CF的值.
,求CF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形纸片ABC中,∠ACB=90°,AC=2,BC=4,点D在边AB上,以CD为折痕将△CBD折叠得到△CPD,CP与边AB交于点E,若△DEP为直角三角形,则BD的长是_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B,
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=![]() ,求⊙O 的半径.
,求⊙O 的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队承接了60万平方米的绿化工程,由于情况有变,……设原计划每天绿化的面积为![]() 万平方米,列方程为
万平方米,列方程为![]() ,根据方程可知省略的部分是( )
,根据方程可知省略的部分是( )
A. 实际工作时每天的工作效率比原计划提高了![]() 结果提前30天完成了这一任务
结果提前30天完成了这一任务
B. 实际工作时每天的工作效率比原计划提高了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
C. 实际工作时每天的工作效率比原计划降低了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
D. 实际工作时每天的工作效率比原计划降低了![]() ,结果提前30天完成了这一任务
,结果提前30天完成了这一任务
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com