
����Ŀ�����ݺ���ѧϰ�л��۵�֪ʶ�뾭�飬����ʦҪ��ѧ��̽������y=![]() +1��ͼ��ͬѧ��ͨ���б�����㡢��ͼ��������ͼ�����������㲹��������
+1��ͼ��ͬѧ��ͨ���б�����㡢��ͼ��������ͼ�����������㲹��������
��1������y=![]() +1��ͼ�������������Ϥ�ĺ����� ����ͼ������ƽ���� ������λ�õ���
+1��ͼ�������������Ϥ�ĺ����� ����ͼ������ƽ���� ������λ�õ���
��2������y=![]() +1��ͼ����x�ᡢy�ύ�������ǣ��� ����
+1��ͼ����x�ᡢy�ύ�������ǣ��� ����
��3�����㹹��һ��������ʹ��ͼ����x��Ľ���Ϊ��2��0��������y�����㣬�����������ʽ�������� ����
���𰸡���1��![]() ��1����2����x�ύ�ڣ���1��0������y��û���㣻��3���𰸲�Ψһ���磺y=��
��1����2����x�ύ�ڣ���1��0������y��û���㣻��3���𰸲�Ψһ���磺y=��![]() +1.
+1.
��������
��1�����ݺ���ͼ���ƽ�ƹ��ɣ��ɵô𰸣�
��2�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵô𰸣�
��3�����ݵ���������㺯������ʽ���ɵô𰸣�
��1������![]() ��ͼ�������������Ϥ�ĺ���
��ͼ�������������Ϥ�ĺ���![]() ��ͼ������ƽ��1����λ�õ���
��ͼ������ƽ��1����λ�õ���
�ʴ�Ϊ��![]() ��1��
��1��
��2������![]() ��ͼ����x�ᡢy�ύ�������ǣ���x�ύ�ڣ���1��0������y��û���㣬
��ͼ����x�ᡢy�ύ�������ǣ���x�ύ�ڣ���1��0������y��û���㣬
�ʴ�Ϊ����x�ύ�ڣ���1��0������y��û���㣻
��3�����㹹��һ��������ʹ��ͼ����x��Ľ���Ϊ��2��0��������y�����㣬�����������ʽ�����ǣ�y=��![]() +1�� �𰸲�Ψһ��
+1�� �𰸲�Ψһ��
�ʴ�Ϊ��y=��![]() +1��
+1��


 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����籭��С����������ĸ���ӽ��е�ѭ��������ÿ������һ������ʤһ����3�֣�ƽһ����1�֣���һ����0��.ijС����������ס��ҡ��������Ķӷֱ��õ�һ�������������������ӵ��ܵ÷�ǡ�����ĸ����������������Ҵ�ƽ������ǣ� ��
A. �� B. ���붡 C. �� D. ���붡
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ��������ԭ�㣬��
��������ԭ�㣬��![]() �����һ������Ϊ
�����һ������Ϊ![]() ���Ҷ���
���Ҷ���![]() ����Ϊ
����Ϊ![]() .
.
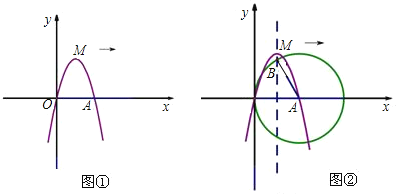
��1���������߽���ʽ.
��2��������������ƽ��![]() ����λ��������������
����λ��������������![]() �ύ��
�ύ��![]() ���㣬��ԭ�����߽��ڵ�
���㣬��ԭ�����߽��ڵ�![]() ����
����![]() �����Ϊ
�����Ϊ![]() ����
����![]() ����
����![]()
![]() �ĺ�����ϵʽ.
�ĺ�����ϵʽ.
��3����ͼ�ڣ��Ե�![]() ΪȦ�ģ����߶�
ΪȦ�ģ����߶�![]() Ϊ�뾶��Բ����������
Ϊ�뾶��Բ����������![]() �ĶԳ����ڵ�
�ĶԳ����ڵ�![]() ������
������![]() ����������������ƽ��
����������������ƽ��![]() ����λ��
����λ��![]() ��Ķ�Ӧ��Ϊ
��Ķ�Ӧ��Ϊ![]() ��
��![]() ��Ķ�Ӧ��Ϊ
��Ķ�Ӧ��Ϊ![]() ���������ı���
���������ı���![]() Ϊ���Σ�ƽ�ƺ�������ߵĶԳ��������εĶԽ���
Ϊ���Σ�ƽ�ƺ�������ߵĶԳ��������εĶԽ���![]() ���ڵ�
���ڵ�![]() �ʣ���
�ʣ���![]() �����Ƿ����һ��
�����Ƿ����һ��![]() ��ʹ����
��ʹ����![]() ��
��![]() �������������
Ϊ�������������![]() ���ƣ������ڣ����F�����꣬�������ڣ���˵������.
���ƣ������ڣ����F�����꣬�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�ı߳�AD��3��AB��2����BAD��120����EΪAB���е㣬F�ڱ�BC�ϣ���BF��2FC��AF��DE���ڵ�G����AG�ij�Ϊ_____��
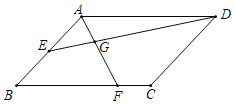
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽��
��ͼ1����ƽ��ֱ������ϵ�У�������y��ax2+![]() x+3��x�ύ��A��B���㣨A��B��ࣩ����y�ύ�ڵ�C����A����Ϊ����1��0����ֱ��lΪ�������ߵĶԳ��ᣬ�ҽ�ֱ��BC�ڵ�D������������һ����P���Һ�����Ϊm��4��m��9��������PD������P��PE��l�ڵ�E��
x+3��x�ύ��A��B���㣨A��B��ࣩ����y�ύ�ڵ�C����A����Ϊ����1��0����ֱ��lΪ�������ߵĶԳ��ᣬ�ҽ�ֱ��BC�ڵ�D������������һ����P���Һ�����Ϊm��4��m��9��������PD������P��PE��l�ڵ�E��
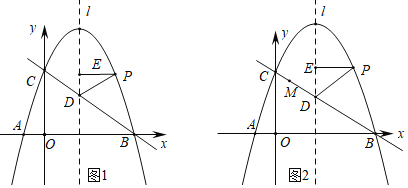
��1����������ֱ��BC�ĺ�������ʽ��
��2������DEP����BOC����ʱ����m��ֵ��
��3����ͼ2����MΪֱ��BC��һ���㣬�Ƿ���ڵ�P��ʹ���Ե�A��C��P��MΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д����ʱ��P�͵�M�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������Ļ�����ʶ��ij�з��������ܼ��ţ���ɫ�������ij�����ij��ҵץס����Ͷ��20��Ԫ����Ͷ��һ��A������������������Ϊ�������������ӣ��ƻ�����Ͷ��B�͵�����B�͵�����Ͷ��������A�͵�����Ͷ��������ͬ��Ͷ���ܷ��ü���20%������B�͵����ĵ��۱ȹ���A�͵����ĵ�����50Ԫ����A�͵���ÿ�����ļ۸��Ƕ���Ԫ����A�͵���ÿ�����ļ۸�ΪxԪ���������⣬�з�����ȷ���ǣ�������
A.![]() ��
��![]()
B.![]() ��
��![]()
C.![]() ��
��![]()
D.![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ȱ���ABC��CD��AB��D��AF��AC��EΪ�߶�CD��һ�㣬��CE��AF������BE��BF��EG��BF��G������DG��
��1����֤��BE��BF��
��2����˵��DG��AF��λ�ù�ϵ��������ϵ��
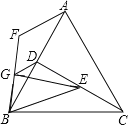
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
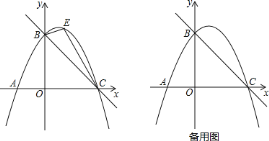
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��������
��������![]() ����
����![]() ��
��![]() ���㣮
���㣮
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
![]() ��ͼ����
��ͼ����![]() ��ֱ��
��ֱ��![]() �Ϸ��������ϵ�һ���㣬��
�Ϸ��������ϵ�һ���㣬��![]() ������ʱ���������
������ʱ���������![]() �������
�������![]() ��������ֵ��
��������ֵ��
![]() ��
��![]() �Ľ����£�����
�Ľ����£�����![]() ��
��![]() ���ƽ���߽�ֱ��
���ƽ���߽�ֱ��![]() �ڵ�
�ڵ�![]() ������
������![]() ����
����![]() �������߶Գ����ϵĶ��㣬�����������Ƿ���ڵ�
�������߶Գ����ϵĶ��㣬�����������Ƿ���ڵ�![]() ��ʹ����
��ʹ����![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı�����ƽ���ı��Σ�������ڣ���ֱ��д����
Ϊ������ı�����ƽ���ı��Σ�������ڣ���ֱ��д����![]() �����ꣻ��������ڣ���˵�����ɣ�
�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
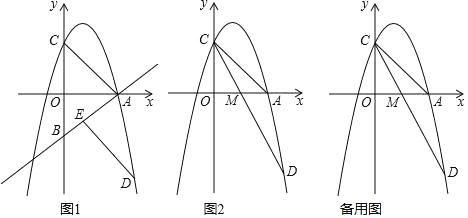
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y��x��3��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B����B����x��ĶԳƵ���C�����κ���y����x2+bx+c��ͼ����A�͵�C��
��1������κ����ı���ʽ��
��2����ͼ1��ƽ���߶�AC����A�Ķ�Ӧ��D���ڶ��κ����ڵ�������ͼ���ϣ���C�Ķ�Ӧ��E����ֱ��AB�ϣ����ʱ��D�����ꣻ
��3����ͼ2���ڣ�2���������£�����CD����CD���ڵ�M����PΪֱ��AC�Ϸ���������һ���㣬����P��PF��AC������Ϊ��F������PC���Ƿ���ڵ�P��ʹ���Ե�P��C��FΪ���������������COM���ƣ������ڣ����P�ĺ����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com