
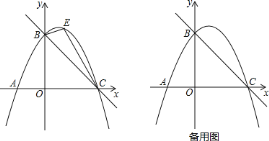
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图,点
如图,点![]() 是直线
是直线![]() 上方抛物线上的一动点,当
上方抛物线上的一动点,当![]() 面积最大时,请求出点
面积最大时,请求出点![]() 的坐标和
的坐标和![]() 面积的最大值?
面积的最大值?
![]() 在
在![]() 的结论下,过点
的结论下,过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,连接
,连接![]() ,点
,点![]() 是抛物线对称轴上的动点,在抛物线上是否存在点
是抛物线对称轴上的动点,在抛物线上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?如果存在,请直接写出点
为顶点的四边形是平行四边形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,即点
时,即点![]() 的坐标是
的坐标是![]() 时,
时,![]() 的面积最大,最大面积是
的面积最大,最大面积是![]() ;(3)点
;(3)点![]() 的坐标是
的坐标是![]() 、
、![]() 、
、![]() .
.
【解析】
(1)首先根据直线y=﹣![]() x+3与x轴交于点C,与y轴交于点B,求出点B的坐标是(0,3),点C的坐标是(4,0);然后根据抛物线y=ax2+
x+3与x轴交于点C,与y轴交于点B,求出点B的坐标是(0,3),点C的坐标是(4,0);然后根据抛物线y=ax2+![]() x+c经过B、C两点,求出a\c的值是多少,即可求出抛物线的解析式.
x+c经过B、C两点,求出a\c的值是多少,即可求出抛物线的解析式.
(2)首先过点E作y轴的平行线EF交直线BC于点M,EF交x轴于点F,然后设点E的坐标是(x,﹣![]() x2+
x2+![]() x+3),则点M的坐标是(x,﹣
x+3),则点M的坐标是(x,﹣![]() x+3),求出EM的值是多少;最后根据三角形的面积的求法,求出S△ABC,进而判断出当△BEC面积最大时,点E的坐标和△BEC面积的最大值各是多少即可.
x+3),求出EM的值是多少;最后根据三角形的面积的求法,求出S△ABC,进而判断出当△BEC面积最大时,点E的坐标和△BEC面积的最大值各是多少即可.
(3)在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形.然后分三种情况讨论,根据平行四边形的特征,求出使得以P、Q、A、M为顶点的四边形是平行四边形的点P的坐标是多少即可.
(1)∵直线y=﹣![]() x+3与x轴交于点C,与y轴交于点B,∴点B的坐标是(0,3),点C的坐标是(4,0).
x+3与x轴交于点C,与y轴交于点B,∴点B的坐标是(0,3),点C的坐标是(4,0).
∵抛物线y=ax2+![]() x+c经过B、C两点,∴
x+c经过B、C两点,∴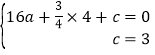 ,解得:
,解得: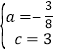 ,∴y=﹣
,∴y=﹣![]() x2+
x2+![]() x+3.
x+3.
(2)如图1,过点E作y轴的平行线EF交直线BC于点M,EF交x轴于点F.
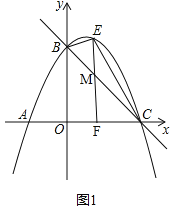
∵点E是直线BC上方抛物线上的一动点,∴设点E的坐标是(x,﹣![]() x2+
x2+![]() x+3),则点M的坐标是(x,﹣
x+3),则点M的坐标是(x,﹣![]() x+3),∴EM=﹣
x+3),∴EM=﹣![]() x2+
x2+![]() x+3﹣(﹣
x+3﹣(﹣![]() x+3)=﹣
x+3)=﹣![]() x2+
x2+![]() x,∴S△BEC=S△BEM+S△MEC
x,∴S△BEC=S△BEM+S△MEC
=![]() =
=![]() ×(﹣
×(﹣![]() x2+
x2+![]() x)×4=﹣
x)×4=﹣![]() x2+3x=﹣
x2+3x=﹣![]() (x﹣2)2+3
(x﹣2)2+3
∴当x=2时,即点E的坐标是(2,3)时,△BEC的面积最大,最大面积是3.
(3)在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形.
①如图2,由(2),可得点M的横坐标是2.
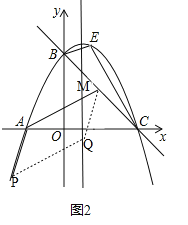
∵点M在直线y=﹣![]() x+3上,∴点M的坐标是(2,
x+3上,∴点M的坐标是(2,![]() ).
).
又∵点A的坐标是(﹣2,0),∴AM=![]() =
=![]() ,∴AM所在的直线的斜率是:
,∴AM所在的直线的斜率是:![]() ;
;
∵y=﹣![]() x2+
x2+![]() x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣
x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣![]() x2+
x2+![]() x+3),则
x+3),则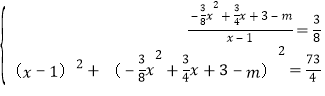
解得: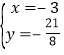 或
或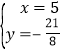 .
.
∵x<0,∴点P的坐标是(﹣3,﹣![]() ).
).
②如图3,由(2),可得点M的横坐标是2.
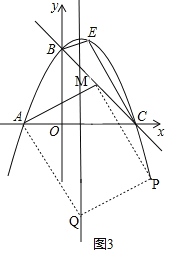
∵点M在直线y=﹣![]() x+3上,∴点M的坐标是(2,
x+3上,∴点M的坐标是(2,![]() ).
).
又∵点A的坐标是(﹣2,0),∴AM=![]() =
=![]() ,∴AM所在的直线的斜率是:
,∴AM所在的直线的斜率是:![]() ;
;
∵y=﹣![]() x2+
x2+![]() x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣
x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣![]() x2+
x2+![]() x+3),则
x+3),则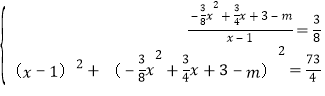
解得: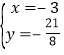 或
或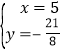 .
.
∵x>0,∴点P的坐标是(5,﹣![]() ).
).
③如图4,由(2),可得点M的横坐标是2.
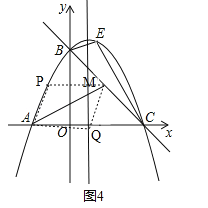
∵点M在直线y=﹣![]() x+3上,∴点M的坐标是(2,
x+3上,∴点M的坐标是(2,![]() ).
).
又∵点A的坐标是(﹣2,0),∴AM=![]() =
=![]() .
.
∵y=﹣![]() x2+
x2+![]() x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣
x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣![]() x2+
x2+![]() x+3),则
x+3),则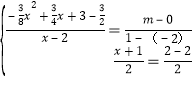 ,解得:
,解得: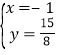 ,∴点P的坐标是(﹣1,
,∴点P的坐标是(﹣1,![]() ).
).
综上,可得在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形,点P的坐标是(﹣3,﹣![]() )、(5,﹣
)、(5,﹣![]() )、(﹣1,
)、(﹣1,![]() ).
).


科目:初中数学 来源: 题型:
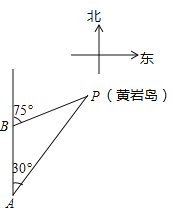
【题目】如图,三沙市一艘海监船某天在黄岩鸟P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据: ![]() ≈1.414,结果精确到0.1)
≈1.414,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级学生乘车去参加社会实践话动,若每辆客车乘50人,还有12人不能上车;若每辆客车乘55人,则最后一辆空了8个座位,求该校租了多少辆客车?七年级学生多少人?
根据题意,小明、小红分别列出了尚不完整的方程如下:
小明:50x口![]()
![]() 口
口![]()
![]() ;小红:
;小红:![]()
(其中“口”表示运算符号,“![]()
![]() ”表示数字)
”表示数字)
![]() 小明所列方程中x表示的意义是:______;小红所列方程中y表示的意义是:______;
小明所列方程中x表示的意义是:______;小红所列方程中y表示的意义是:______;
![]() 请你把小明或小红所列方程补充完整,并相应解答.
请你把小明或小红所列方程补充完整,并相应解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
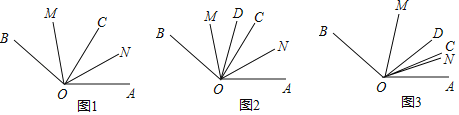
【题目】已知:∠AOB=140°,OC,OM,ON是∠AOB内的射线.
(1)如图1所示,若OM平分∠BOC,ON平分∠AOC,求∠MON的度数:
(2)如图2所示,OD也是∠AOB内的射线,∠COD=15°,ON平分∠AOD,OM平分∠BOC.当∠COD绕点O在∠AOB内旋转时,∠MON的位置也会变化但大小保持不变,请求出∠MON的大小;
(3)在(2)的条件下,以∠AOC=20°为起始位置(如图3),当∠COD在∠AOB内绕点O以每秒3°的速度逆时针旋转t秒,若∠AON:∠BOM=19:12,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于一个有理数x,我们把[x]称作x的对称数.
若![]() ,则[x]=x-2:若x<0,则[x]=x+2.例:[1]=1-2=-1,[-2]=-2+2=0
,则[x]=x-2:若x<0,则[x]=x+2.例:[1]=1-2=-1,[-2]=-2+2=0
(1)求[![]() ][-1]的值;
][-1]的值;
(2)已知有理数a>0.b<0,且满足[a]=[b],试求代数式![]() 的值:
的值:
(3)解方程:[2x]+[x+1]=1
查看答案和解析>>
科目:初中数学 来源: 题型:
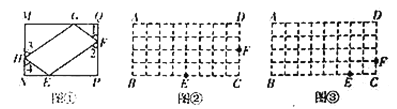
【题目】(问题原型)在图①的矩形![]() 中,点
中,点![]() 、
、![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 、
、![]() 上,若
上,若![]() ,则称四边形
,则称四边形![]() 为矩形
为矩形![]() 的反射四边形;
的反射四边形;
(操作与探索)在图②,图③的矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边的格点上,试利用正方形网格分别在图②、图③上作矩形
边的格点上,试利用正方形网格分别在图②、图③上作矩形![]() 的反射四边形
的反射四边形![]() ;
;
(发现与应用)由前面的操作可以发现,一个矩形有不同的反射四边形,且这些反射四边形的周长都相等.若在图①的矩形![]() 中,
中,![]() ,
,![]() ,则其反射四边形
,则其反射四边形![]() 的周长为______.
的周长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠A=90°.
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明);
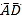
(2)在(1)的条件下,若∠B=45°,AB=1,⊙P切BC于点D,求劣弧![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
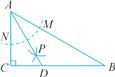
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧,分别交AB,AC于点M和N,再分别以点M,N为圆心,大于![]() MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的个数是( )
MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC∶S△ABC=1∶3.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com