
【题目】如图,已知在△ABC中,∠A=90°.
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明);
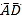
(2)在(1)的条件下,若∠B=45°,AB=1,⊙P切BC于点D,求劣弧![]() 的长.
的长.
【答案】(1)画图见解析;(2)(2)弧AD的长为![]() π.
π.
【解析】分析: (1)作∠ABC的平分线,与AC的交点就是圆心P,此时⊙P与AB,BC两边都相切;如图,作BC的垂线PD,证明PD和半径相等即可,根据角平分线的性质可得:PA=PD.
(2)要想求劣弧AD的长,根据弧长公式需求圆心角∠APD的半径AP的长,利用四边形的内角和求∠APD=135°,再利用勾股定理和等腰三角形的性质求出AP=PD=DC=![]() 1,代入公式可求弧长.
1,代入公式可求弧长.
详解:
(1)作∠ABC的角平分线交AC于点P,以点P为圆心,AP为半径作圆.
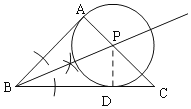
(2)如图,∵P与AB,BC两边都相切,
∴∠BAP=∠BDP=90°,
∵∠ABC=45°,
∴∠APD=360°90°90°45°=135°,
∴∠DPC=45°,
∴△DPC是等腰直角三角形,
∴DP=DC,
在Rt△ABC中,AB=AC=1,
∴CB=![]() ,
,
∵BP=BP,AP=PD,
∴Rt△ABP≌Rt△DBP,
∴BD=AB=1,
∴CD=PD=AP=![]() 1,
1,
∴劣弧AD的长=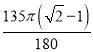 =
=![]() .
.
点睛: 本题考查了切线的判定、圆的作图以及弧长的计算,首先掌握切线的判定方法:①无交点,作垂线段,证半径;②有交点,作半径,证垂直;本题利用了第①种判定方法;并熟练掌握弧长计算公式:l=![]() (弧长为l,圆心角度数为n,圆的半径为R).
(弧长为l,圆心角度数为n,圆的半径为R).


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】“食品安全”受到全社会的广泛关注,济南市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两份尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题.
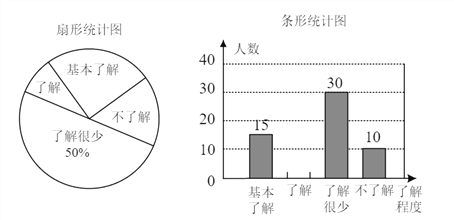
(1)接受问卷调查的学生共有_____人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_____.
(2)请补全条形统计图.
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数.
(4)若从对食品安全知识达到“了解”程度的2个女生和2个男生中随机抽取2人参加食品安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
【答案】(1)60;90°;(2)补图见解析;(3)300;(4)![]()
【解析】分析:(1)根据了解很少的人数除以了解很少的人数所占的百分百求出抽查的总人数,再用“基本了解”所占的百分比乘以360°,即可求出“基本了解”部分所对应扇形的圆心角的度数;(2)用调查的总人数减去“基本了解”“了解很少”和“基本了解”的人数,求出了解的人数,从而补全统计图;(3)用总人数乘以“了解”和“基本了解”程度的人数所占的比例,即可求出达到“了解”和“基本了解”程度的总人数;(4)根据题意列出表格,再根据概率公式即可得出答案.
详解:(1)60;90°.
(2)补全的条形统计图如图所示.
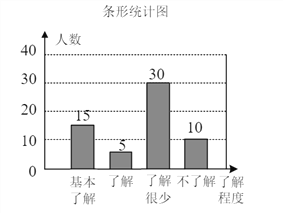
(3)对食品安全知识达到“了解”和“基本了解”的学生所占比例为![]() ,由样本估计总体,该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数为
,由样本估计总体,该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数为![]() .
.
(4)列表法如表所示,
男生 | 男生 | 女生 | 女生 | |
男生 | 男生男生 | 男生女生 | 男生女生 | |
男生 | 男生男生 | 男生女生 | 男生女生 | |
女生 | 男生女生 | 男生女生 | 女生女生 | |
女生 | 男生女生 | 女生女生 |
所有等可能的情况一共12种,其中选中1个男生和1个女生的情况有8种,所以恰好选中1个男生和1个女生的概率是![]() .
.
点睛:本题考查了条形统计图、扇形统计图以及用列表法或树状图法求概率,根据题意求出总人数是解题的关键;注意运用概率公式:概率=所求情况数与总情况数之比.
【题型】解答题
【结束】
24
【题目】为响应国家全民阅读的号召,某社区鼓励居民到社区阅览室借阅读书,并统计每年的借阅人数和图书借阅总量(单位:本),该阅览室在2015年图书借阅总量是7500本,2017年图书借阅总量是10800本.
(1)求该社区的图书借阅总量从2015年至2017年的年平均增长率.
(2)已知2017年该社区居民借阅图书人数有1350人,预计2018年达到1440人,如果2017年至2018年图书借阅总量的增长率不低于2015年至2017年的年平均增长率,设2018年的人均借阅量比2017年增长a%,求a的值至少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:①当x=1时,点P是正方形ABCD的中心;②当x=![]() 时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是3;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确的选项是( )
时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是3;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确的选项是( )
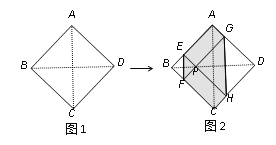
A. ①③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为﹣7,点B表示的数为5,点C到点A,点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动的时间为t(t>0)秒.
(1)点C表示的数是 ;
(2)求当t等于多少秒时,点P到达点B处;
(3)点P表示的数是 (用含有t的代数式表示);
(4)求当t等于多少秒时,PC之间的距离为2个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
科目:初中数学 来源: 题型:
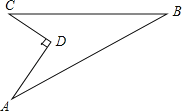
【题目】(本题8分)如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“垃圾分类”越来越受到人们的关注,我市某中学对部分学生就“垃圾分类”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:
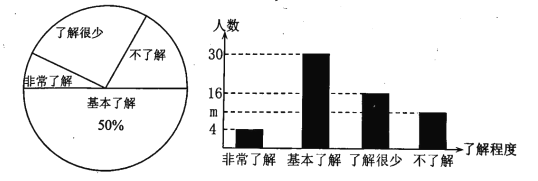
(1)接受问卷调查的学生共有________人,条形统计图中m的值为_______;
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为________;
(3)若该校学生总数为1200人,试估计该校学生中对垃圾分类知识达到“非常了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行猜谜语大赛,甲、乙两队各有5名选手参赛。他们的成绩(满分100分,两个1号队员的成绩均未统计)如图所示

成绩统计分析表:
平均数 | 中位数 | 众数 | 方差 | 优秀率 | |
甲队 | 85 | 85 | 70 | 80% | |
乙队 | 85 | 160 |
根据以上材料
(1)计算出甲、乙两队1号选手的成绩;
(2)补充完成成绩统计图和成绩统计分析表.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com