
����Ŀ��������������Խ��Խ�ܵ����ǵĹ�ע������ij��ѧ�Բ���ѧ����������������֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ.����ͼ����Ϣ�ش��������⣺
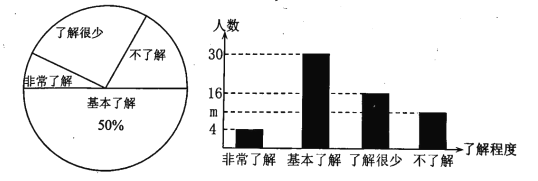
��1�������ʾ������ѧ������________�ˣ�����ͳ��ͼ��m��ֵΪ_______��
��2������ͳ��ͼ�����˽��������������Ӧ���ε�Բ�ĽǵĶ���Ϊ________��
��3������Уѧ������Ϊ1200�ˣ��Թ��Ƹ�Уѧ���ж���������֪ʶ�ﵽ���dz��˽������������˽����̶ȵ�������.
���𰸡���1��60��10����2��96�㣻��3��680��.
��������
��1���á������˽⡱��������������ռ�İٷֱȵõ��������������������������ȥ������������������ɵõ�m��ֵ��
��2����360���������ͳ��ͼ�С��˽���١�������ռ�ı������ɣ�
��3����������1200���Դﵽ���dz��˽⡱�͡������˽⡱�̶ȵ�������ռ�ı������ɣ�
�⣺��1��������Ϊ��![]() ���ˣ���
���ˣ���
![]() ��
��
�ʴ�Ϊ��60��10��
��2�����˽���١���Բ�Ľ�Ϊ��![]() ��
��
�ʴ�Ϊ��96�㣻
��3����Уѧ���ж���������֪ʶ�ﵽ���dz��˽������������˽����̶ȵ�������Ϊ��
![]() ���ˣ�.
���ˣ�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ڿ������п�������һ���������Ļ�������⣺
���㣺![]()
�����֣������ʽ��ӳ����ǰ�������ֵĺͣ�����������֮�������ij�ֹ�ϵ���������ֹ�ϵ����˳���ؽ��������⡣
��1��ǰ��������֮�������ʲô��ϵ��
��2���ȼ����IJ��ֱȽϼ�㣿�������Ƚϼ����Dz��֡�
��3�����ã�1���еĹ�ϵ��ֱ��д����һ���ֵĽ����
��4���������Ϸ��������ԭʽ�Ľ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
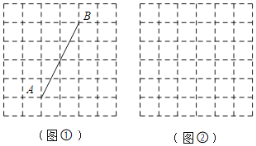
����Ŀ����ͼ�������������У�ÿ��С�����εı߳���Ϊ1��ÿ��С�����εĶ���и�㣮
��1����ͼ���У��߶�AB�ij���Ϊ ������ͼ�л�����CΪֱ�Ƕ����Rt��ABC��ʹ��C�ڸ���ϣ�����ͼ�л������е�C��
��2����ͼ���У��Ը��Ϊ���㣬�������̶ȵ�ֱ��������ABCD��ʹ�������Ϊ13���ٻ�һ��ֱ��PQ�����������ζԽ����غϣ���ʹPQǡ�ý�������ABCD��������ȷ֣�������ͼ�ۼ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABC�У���A=90����
��1������Բ���ֱ��������P��ʹԲ��P��AC���ϣ�����AB��BC���߶����У�������ͼ�ۼ�����д������֤������
��2���ڣ�1���������£�����B=45����AB=1����P��BC�ڵ�D�����ӻ�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+4��ͼ����x�ύ������A��B����y�ύ�ڵ�C����A����1��0����B��4��0����
��1����˶��κ����ı���ʽ��
��2����ͼ1�������ߵĶԳ���m��x�ύ�ڵ�E��CD��m������ΪD����F����![]() ��0��������N���߶�DE���˶�������CF��CN��FN�����Ե�C��D��NΪ���������������FEN���ƣ����N�����ꣻ
��0��������N���߶�DE���˶�������CF��CN��FN�����Ե�C��D��NΪ���������������FEN���ƣ����N�����ꣻ
��3����ͼ2����M���������ϣ��ҵ�M�ĺ�������1��������MA�Ƶ�M��ʱ����ת45�������������ڵ�P�����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��B�������ϱ�ʾ����a��b,����![]()
��1��a��ֵΪ______��b��ֵΪ______��
��2����֪��M����N�������ϵ��������㣬��M�ӵ�A�������ٶ���ÿ��3����λ��ͬʱ��N�ӵ�B�������ٶ���ÿ��1����λ��
�� ����M�͵�N�������������˶�������t����C����������t��ֵ�ʹ�ʱ��C����ʾ������
�� ����M�͵�N����������������ͬ���˶������������룬��M�͵�N���2����λ�����ʱ��M�͵�N��ʾ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2016�����������У��Ͷ����ʹ���ֻ��Ϳ���ʱ�õĹ���������ij��Ӫ��Ϊ����侭Ӫ��AƷ�ƹ����������г�ռ���ʣ������շ������µ�����һ���У�ͬһ���˵�һ��ʹ�õij��Ѱ�0.5Ԫ��ȡ��ÿ����һ�Σ����γ��Ѿͱ��ϴγ��Ѽ���0.1Ԫ����6�ο�ʼ�������ó���ѡ������շѱ����£�

ͬʱ���ʹ��շѷ������������ij��У100��ʦ����һ����ʹ��AƷ�ƹ�����������Ը���õ��������ݣ�

��1��д��a��b��ֵ��
��2����֪��У��5100��ʦ������AƷ�ƹ�������Ͷ�Ÿ�Уһ��ķ���Ϊ5800Ԫ���Թ��ƣ��շѵ�������Ӫ���ڸ�УͶ��AƷ�ƹ��������ܷ������˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=BC=4��AO=BO��P������CO�ϵ�һ�����㣬��AOC=60��������PABΪֱ��������ʱ��AP�ij�Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���A����ABC��90����AD��1��BC��3����E�DZ�CD���е㣬����BE���ӳ���AD���ӳ����ڵ�F������CF��
(1)��֤���ı���BDFC��ƽ���ı��Σ�
(2)��CB��CD�����ı���BDFC�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com