
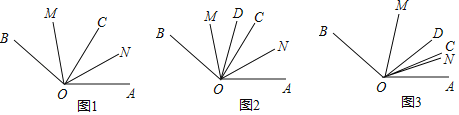
【题目】已知:∠AOB=140°,OC,OM,ON是∠AOB内的射线.
(1)如图1所示,若OM平分∠BOC,ON平分∠AOC,求∠MON的度数:
(2)如图2所示,OD也是∠AOB内的射线,∠COD=15°,ON平分∠AOD,OM平分∠BOC.当∠COD绕点O在∠AOB内旋转时,∠MON的位置也会变化但大小保持不变,请求出∠MON的大小;
(3)在(2)的条件下,以∠AOC=20°为起始位置(如图3),当∠COD在∠AOB内绕点O以每秒3°的速度逆时针旋转t秒,若∠AON:∠BOM=19:12,求t的值.
【答案】(1)∠MON的度数为70°.(2)∠MON的度数为62.5°.(3)t的值为20.
【解析】
(1)根据角平分线的性质以及角的和差倍关系转化求出角的度数;
(2)根据角平分线的性质可以求得:∠MON=![]() (∠AOB+∠COD)﹣∠COD,代入数据即可求得;
(∠AOB+∠COD)﹣∠COD,代入数据即可求得;
(3)由题意得∠AON=![]() (20°+3t+15°),∠BOM=
(20°+3t+15°),∠BOM=![]() (140°﹣20°﹣3t),由此列出方程即可求解.
(140°﹣20°﹣3t),由此列出方程即可求解.
(1)∵ON平分∠AOC,OM平分∠BOC,
∴∠CON=![]() ∠AOC,∠COM=
∠AOC,∠COM=![]() ∠BOC
∠BOC
∠MON=∠CON+∠COM
=![]() (∠AOC+∠BOC)
(∠AOC+∠BOC)
=![]() ∠AOB
∠AOB
又∠AOB=140°
∴∠MON=70°
答:∠MON的度数为70°.
(2)∵OM平分∠BOC,ON平分∠AOD,
∴∠COM=![]() ∠BOC,∠DON=
∠BOC,∠DON=![]() ∠AOD
∠AOD
即∠MON=∠COM+∠DON﹣∠COD
=![]() ∠BOC+
∠BOC+![]() ∠AOD﹣∠COD
∠AOD﹣∠COD
=![]() (∠BOC+∠AOD)﹣∠COD.
(∠BOC+∠AOD)﹣∠COD.
=![]() (∠BOC+∠AOC+∠COD)﹣∠COD
(∠BOC+∠AOC+∠COD)﹣∠COD
=![]() (∠AOB+∠COD)﹣∠COD
(∠AOB+∠COD)﹣∠COD
=![]() (140°+15°)﹣15°
(140°+15°)﹣15°
=62.5°
答:∠MON的度数为62.5°.
(3)∠AON=![]() (20°+3t+15°),
(20°+3t+15°),
∠BOM=![]() (140°﹣20°﹣3t)
(140°﹣20°﹣3t)
又∠AON:∠BOM=19:12,
12(35°+3t)=19(120°﹣3t)
得t=20
答:t的值为20.



 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
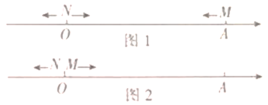
【题目】数轴上点A表示的数为10,点M,N分别以每秒a个单位长度,每秒b个单位长度的速度沿数轴运动,a, b满足|a-5|+(b-6)2=0.
(1)请真接与出a= , b= ;
(2)如图1,点M从A出发沿数轴向左运动,到达原点后立即返回向右运动:同时点N从原点0出发沿数轴向左运动,运动时间为t,点P为线段ON的中点若MP=MA,求t的值:
(3)如图2,若点M从原点向右运动,同时点N从原点向左运动,运动时间为t时M运动到点A的右侧,若此时以M,N, O, A为端点的所有线段的长度和为142,求此时点M对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
如图①,若点B把线段分成两条长度相等的线段AB和BC,则点B叫做线段AC的中点.
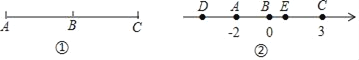
回答问题:
(1)如图②,在数轴上,点A所表示的数是﹣2,点B所表示的数是0,点C所表示的数是3.
①若A是线段DB的中点,则点D表示的数是 ;
②若E是线段AC的中点,求点E表示的数.
(2)在数轴上,若点M表示的数是m,点N所表示的数是n,点P是线段MN的中点.
①若点P表示的数是1,则m、n可能的值是 (填写符合要求的序号);
(i)m=0,n=2;(ii)m=﹣5,n=7;(iii)m=0.5,n=1.5;(iv)m=﹣1,n=2
②直接用含m、n的代数式表示点P表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿谷商场“家电下乡”指定型号冰箱、彩电的进价和售价如下表所示:
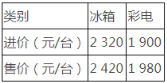
(1)按国家政策,农民购买“家电下乡”产品可享受售价13%的政府补贴.农民田大伯到该商场购买了冰箱、彩电各一台,可以享受多少元的政府补贴?
(2)为满足农民需求,商场决定用不超过85000元采购冰箱、彩电共40台,且冰箱的数量不少于彩电数量的![]() .
.
①请你帮助该商场设计相应的进货方案;
②哪种进货方案商场获得利润最大(利润=售价-进价),最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,边OA,OC分别在x轴,y轴的正半轴上,把正方形OABC的内部及边上,横、纵坐标均为整数的点称为好点.点P为抛物线![]() 的顶点.
的顶点.
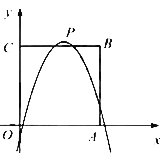
(1)当![]() 时,求该抛物线下方(包括边界)的好点个数.
时,求该抛物线下方(包括边界)的好点个数.
(2)当![]() 时,求该抛物线上的好点坐标.
时,求该抛物线上的好点坐标.
(3)若点P在正方形OABC内部,该抛物线下方(包括边界)恰好存在8个好点,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
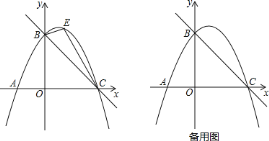
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图,点
如图,点![]() 是直线
是直线![]() 上方抛物线上的一动点,当
上方抛物线上的一动点,当![]() 面积最大时,请求出点
面积最大时,请求出点![]() 的坐标和
的坐标和![]() 面积的最大值?
面积的最大值?
![]() 在
在![]() 的结论下,过点
的结论下,过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,连接
,连接![]() ,点
,点![]() 是抛物线对称轴上的动点,在抛物线上是否存在点
是抛物线对称轴上的动点,在抛物线上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?如果存在,请直接写出点
为顶点的四边形是平行四边形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
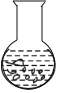
【题目】寓言故事《乌鸦喝水》教导我们遇到困难要运用智慧、认真思考才能让问题迎刃而解.如图,一个紧口瓶中盛有一些水,可乌鸦的嘴够不到瓶中的水.于是乌鸦衔来一些小石子放入瓶中,瓶中的水面高度得到提升.由于放入的石子较多,水都快溢出来了,乌鸦成功喝到了水,如果衔入瓶中石子的体积为![]() ,水面高度为
,水面高度为![]() ,下面图象能大致表示该故事情节的是( )
,下面图象能大致表示该故事情节的是( )
A.  B.
B. 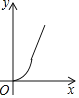 C.
C. 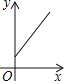 D.
D. 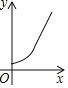
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.
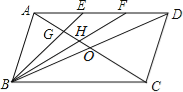
(1)求EG:BG的值;
(2)求证:AG=OG;
(3)设AG=a,GH=b,HO=c,求a:b:c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com