
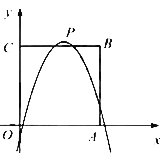
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,边OA,OC分别在x轴,y轴的正半轴上,把正方形OABC的内部及边上,横、纵坐标均为整数的点称为好点.点P为抛物线![]() 的顶点.
的顶点.
(1)当![]() 时,求该抛物线下方(包括边界)的好点个数.
时,求该抛物线下方(包括边界)的好点个数.
(2)当![]() 时,求该抛物线上的好点坐标.
时,求该抛物线上的好点坐标.
(3)若点P在正方形OABC内部,该抛物线下方(包括边界)恰好存在8个好点,求m的取值范围.
【答案】(1)好点有:![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,共5个;(2)
,共5个;(2)![]() ,
,![]() 和
和![]() ;(3)
;(3)![]() .
.
【解析】
(1)如图1中,当m=0时,二次函数的表达式y=﹣x2+2,画出函数图象,利用图象法解决问题即可;(2)如图2中,当m=3时,二次函数解析式为y=﹣(x﹣3)2+5,如图2,结合图象即可解决问题;(3)如图3中,抛物线的顶点P(m,m+2),推出抛物线的顶点P在直线y=x+2上,由点P在正方形内部,则0<m<2,如图3中,E(2,1),F(2,2),观察图象可知,当点P在正方形OABC内部,该抛物线下方(包括边界)恰好存在8个好点时,抛物线与线段EF有交点(点F除外),求出抛物线经过点E或点F时Dm的值,即可判断.
解:(1)当![]() 时,二次函数的表达式为
时,二次函数的表达式为![]()
画出函数图像(图1)
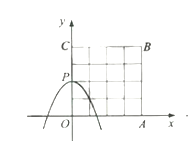
图1
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 抛物线经过点
抛物线经过点![]() 和
和![]()
![]() 好点有:
好点有:![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,共5个
,共5个
(2)当![]() 时,二次函数的表达式为
时,二次函数的表达式为![]()
画出函数图像(图2)
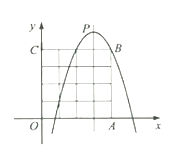
图2
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 该抛物线上存在好点,坐标分别是
该抛物线上存在好点,坐标分别是![]() ,
,![]() 和
和![]()
(3)![]() 抛物线顶点P的坐标为
抛物线顶点P的坐标为![]()
![]() 点P支直线
点P支直线![]() 上
上
由于点P在正方形内部,则![]()
如图3,点![]() ,
,![]()
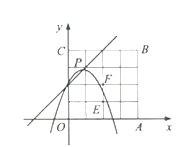
图3
![]() 当顶点P支正方形OABC内,且好点恰好存在8个时,抛物线与线段EF有交点(点F除外)
当顶点P支正方形OABC内,且好点恰好存在8个时,抛物线与线段EF有交点(点F除外)
当抛物线经过点![]() 时,
时,![]()
解得:![]() ,
,![]() (舍去)
(舍去)
当抛物线经过点![]() 时,
时,![]()
解得:![]() ,
,![]() (舍去)
(舍去)
![]() 当
当![]() 时,顶点P在正方形OABC内,恰好存在8个好点
时,顶点P在正方形OABC内,恰好存在8个好点


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到购买某种本子30个和某种笔10支共需280元;购买某种本子50个和某种笔20枝共需500元。
(1)求这种本子和笔的单价;
(2)该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②b24ac<0;③4a+c>2b;④(a+c)2>b2;⑤x(ax+b)ab其中正确结论的是___.
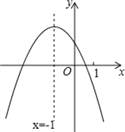
A. ①②⑤ B. ②③④ C. ①③⑤ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级组织知识竞赛,共设20道选择题,各题分值相同,每题必答.右表记录了5个参赛学生的得分情况.问:
参赛者 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
C | 18 | 2 | 88 |
D | 14 | 6 | 64 |
E | 10 | 10 | 40 |
(1)答对一题得 分,答错一题得 分;
(2)有一同学说:同学甲得了70分,同学乙得了90分,你认为谁的成绩是准确的?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB=140°,OC,OM,ON是∠AOB内的射线.
(1)如图1所示,若OM平分∠BOC,ON平分∠AOC,求∠MON的度数:
(2)如图2所示,OD也是∠AOB内的射线,∠COD=15°,ON平分∠AOD,OM平分∠BOC.当∠COD绕点O在∠AOB内旋转时,∠MON的位置也会变化但大小保持不变,请求出∠MON的大小;
(3)在(2)的条件下,以∠AOC=20°为起始位置(如图3),当∠COD在∠AOB内绕点O以每秒3°的速度逆时针旋转t秒,若∠AON:∠BOM=19:12,求t的值.
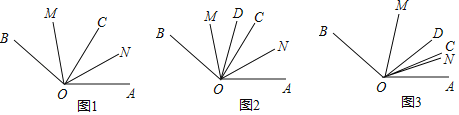
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是![]() =610千克,
=610千克, ![]() =609千克,亩产量的方差分别是
=609千克,亩产量的方差分别是![]() =29.6,
=29.6, ![]() =2.则关于两种小麦推广种植的合理决策是( )
=2.则关于两种小麦推广种植的合理决策是( )
A. 甲的平均亩产量较高,应推广甲
B. 甲、乙的平均亩产量相差不多,均可推广
C. 甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D. 甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给正五边形的顶点依次编号为1,2,3,4,5,若从某一个顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”,如:小明在编号为2的顶点上时,那么他应走2个边长,即从2→3→4为第一次“移位”,这时他到达编号为4的顶点,接下来他应走4个边长后从4→5→1→2→3为第二次“移位”若小明从编号为1的顶点开始,第2020次“移位”后,则他所处顶点的编号为
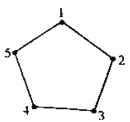
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com