
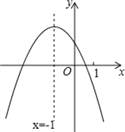
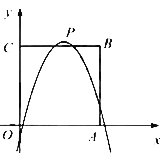
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②b24ac<0;③4a+c>2b;④(a+c)2>b2;⑤x(ax+b)ab其中正确结论的是___.
A. ①②⑤ B. ②③④ C. ①③⑤ D. ③④⑤
【答案】C
【解析】分析:①根据抛物线的开口方向确定a的符号,与y轴的交点确定c的符号,对称轴在y轴的左侧确定b的符号;②由抛物线与x轴的交点的个数确定;③判断当x=-2时的函数值;④判断当x=-1时,a+c与b的关系,注意b的符号;⑤当x=-1时,函数取最大值,所以ax2+bx+c≤a-b+c.
详解:①因为抛物线开口向下,所以a<0;
因为抛物线与y轴交点在y轴的正半轴上,所以c>0;
因为对称轴x=![]() =-1,即b=2a,而a<0,所以b<0,
=-1,即b=2a,而a<0,所以b<0,
所以abc>0.
则①正确;
②因为抛物线与x轴有两个交点,所以b24ac>0.
则②错误;
③因为对称轴x=-1,所以坐标(-2,0)的点与(0,0)关于x=-1对称.
所以当x=-2时,(-2)2a+(-2)b+c>,即4a-2b+c>0,所以4a+c>2b.
则③正确;
④因为当x=-1时,a-b+c>0,所以a+c>b,但b<0,则不能确定(a+c)2与b2的大小.
则④不正确;
⑤当x=-1时,y有最大值是y=a-b+c,
所以ax2+bx+c≤a-b+c,即x(ax+b)≤a-b.
则⑤正确.
故选C.


科目:初中数学 来源: 题型:
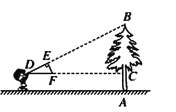
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树AB的高度,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个正方体的平面展开图,标注了字母M的是正方体的正面,如果正方体的左面与右面标注的式子相等.
(1)求x的值;
(2)求正方体的上面和底面的数字和.
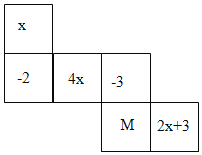
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题:
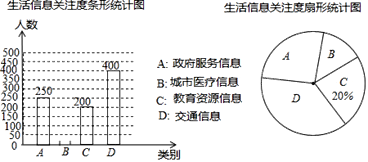
(1)本次参与调查的人数有______ 人;
(2)关注城市医疗信息的有______ 人,并补全条形统计图;
(3)扇形统计图中,D部分的圆心角是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
如图①,若点B把线段分成两条长度相等的线段AB和BC,则点B叫做线段AC的中点.
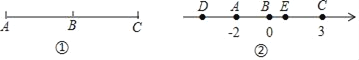
回答问题:
(1)如图②,在数轴上,点A所表示的数是﹣2,点B所表示的数是0,点C所表示的数是3.
①若A是线段DB的中点,则点D表示的数是 ;
②若E是线段AC的中点,求点E表示的数.
(2)在数轴上,若点M表示的数是m,点N所表示的数是n,点P是线段MN的中点.
①若点P表示的数是1,则m、n可能的值是 (填写符合要求的序号);
(i)m=0,n=2;(ii)m=﹣5,n=7;(iii)m=0.5,n=1.5;(iv)m=﹣1,n=2
②直接用含m、n的代数式表示点P表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·漳州)(满分8分)漳州市某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:
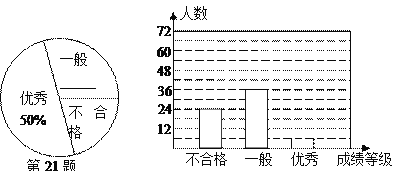
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有_ ▲ 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,边OA,OC分别在x轴,y轴的正半轴上,把正方形OABC的内部及边上,横、纵坐标均为整数的点称为好点.点P为抛物线![]() 的顶点.
的顶点.
(1)当![]() 时,求该抛物线下方(包括边界)的好点个数.
时,求该抛物线下方(包括边界)的好点个数.
(2)当![]() 时,求该抛物线上的好点坐标.
时,求该抛物线上的好点坐标.
(3)若点P在正方形OABC内部,该抛物线下方(包括边界)恰好存在8个好点,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年是我们伟大祖国建国70周年,各种欢庆用品在网上热销.某网店销售甲、乙两种纪念商品,甲种商品每件进价150元,可获利润40元;乙种商品每件进价100元,可获利润30元.由于这两种商品特别畅销,网店老板计划再购进两种商品共100件,其中乙种商品不超过36件.
(1)若购进这100件商品的费用不得超过13700元,求共有几种进货方案?
(2)在(1)的条件下,该网店在71建党节当天对甲种商品以每件优惠m(0<m<20)元的价格进行优惠促销活动,乙种商品价格不变,那么该网店应如何调整进货方案才能获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com